题目内容
4.若直线ax+by=4与不等式组$\left\{\begin{array}{l}2x-5y+8≥0\\ 2x+y-4≤0\\ x+2y+4≥0\end{array}\right.$表示的平面区域无公共点,则a+b的取值范围是(-3,3).分析 由题意画出不等式组$\left\{\begin{array}{l}2x-5y+8≥0\\ 2x+y-4≤0\\ x+2y+4≥0\end{array}\right.$表示的平面区域,结合直线ax+by=4与不等式组$\left\{\begin{array}{l}2x-5y+8≥0\\ 2x+y-4≤0\\ x+2y+4≥0\end{array}\right.$表示的平面区域无公共点得到关于a,b的不等式组,然后利用线性规划知识求得a+b的取值范围.
解答  解:由不等式组$\left\{\begin{array}{l}2x-5y+8≥0\\ 2x+y-4≤0\\ x+2y+4≥0\end{array}\right.$作出平面区域如图,
解:由不等式组$\left\{\begin{array}{l}2x-5y+8≥0\\ 2x+y-4≤0\\ x+2y+4≥0\end{array}\right.$作出平面区域如图,
联立$\left\{\begin{array}{l}{2x-5y+8=0}\\{x+2y+4=0}\end{array}\right.$,解得A(-4,0),
联立$\left\{\begin{array}{l}{2x-5y+8=0}\\{2x+y-4=0}\end{array}\right.$,解得C(1,2),
联立$\left\{\begin{array}{l}{x+2y+4=0}\\{2x+y-4=0}\end{array}\right.$,解得B(4,-4).
∵直线ax+by=4与不等式组$\left\{\begin{array}{l}2x-5y+8≥0\\ 2x+y-4≤0\\ x+2y+4≥0\end{array}\right.$表示的平面区域无公共点,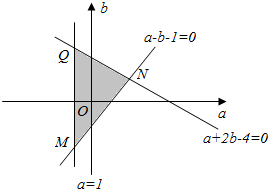 ∴$\left\{\begin{array}{l}{-4a>4}\\{a+2b>4}\\{4a-4b>4}\end{array}\right.$①或$\left\{\begin{array}{l}{-4a<4}\\{a+2b<4}\\{4a-4b<4}\end{array}\right.$②.
∴$\left\{\begin{array}{l}{-4a>4}\\{a+2b>4}\\{4a-4b>4}\end{array}\right.$①或$\left\{\begin{array}{l}{-4a<4}\\{a+2b<4}\\{4a-4b<4}\end{array}\right.$②.
(a,b)所在平面区域如图,
联立$\left\{\begin{array}{l}{a=-1}\\{a-b-1=0}\end{array}\right.$,解得M(-1,-2),
联立$\left\{\begin{array}{l}{a-b-1=0}\\{a+2b-4=0}\end{array}\right.$,解得N(2,1),
令t=a+b,即b=-a+t,
∴当直线b=-a+t过M时,t有最小值为-3;当直线b=-a+t过N时t有最大值为3.
∴t=a+b的范围是(-3,3).
故答案为:(-3,3).
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
| A. | y=3x+5 | B. | y=-3x+5 | C. | y=3x-1 | D. | y=2x |
| A. | f(x)(在(0,$\frac{π}{6}$)单调递增 | B. | f(x)在(-$\frac{π}{3}$,-$\frac{π}{6}$)单调递减 | ||
| C. | f(x)在(-$\frac{π}{6}$,0)单调递减 | D. | f(x)在($\frac{π}{6}$,$\frac{π}{3}$)单调递增 |
| A. | ($\frac{1}{4},1$] | B. | (1,$\frac{3}{2}$] | C. | ($\frac{3}{2},\frac{8}{5}$] | D. | (2,3] |