题目内容
【题目】△ABC的内角A. B. C的对边分别为a,b,c,己知![]() =b(
=b(![]() c-asinC)。
c-asinC)。
(1)求角A的大小;
(2)若b+c=![]() ,
,![]() ,求△ABC的面积。
,求△ABC的面积。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由条件可得![]() ccosA=
ccosA=![]() c-asinC.由正弦定理得sinA+
c-asinC.由正弦定理得sinA+![]() cosA=
cosA=![]() .化简得sin(A+
.化简得sin(A+![]() )=
)=![]() ,解得A即可.
,解得A即可.
(2)由余弦定理得3=b2+c2-bc,即3=(b+c)2-3bc,又b+c=![]() ,解得bc=
,解得bc=![]() .可求△ABC面积.
.可求△ABC面积.
(1)∵ ![]() ,
,
∴ ![]() cbcosA=b(
cbcosA=b(![]() c-asinC),
c-asinC),
即![]() ccosA=
ccosA=![]() c-asinC.由正弦定理得
c-asinC.由正弦定理得![]() sinCcosA=
sinCcosA=![]() sinC-sinAsinC,
sinC-sinAsinC,
∵ sinC![]() 0,
0,
∴ ![]() cosA=
cosA=![]() -sinA,即sinA+
-sinA,即sinA+![]() cosA=
cosA=![]() .
.
所以![]() sinA+
sinA+![]() cosA=
cosA=![]() ,即sin(A+
,即sin(A+![]() )=
)=![]() .
.
∵ 0<A<![]() ,∴
,∴ ![]() .∴ A+
.∴ A+![]() =
=![]() ,即A=
,即A=![]() .
.
(2)在△ABC中,由余弦定理得 a2=b2+c2-2bccosA,
由(1)得A=![]() ,所以a2=b2+c2-2bccos
,所以a2=b2+c2-2bccos![]() ,即a2=b2+c2-bc. ∵ a=
,即a2=b2+c2-bc. ∵ a=![]() ,
,
∴ 3=b2+c2-bc,即3=(b+c)2-3bc.
已知b+c=![]() ,解得bc=
,解得bc=![]() . 所以△ABC的面积为
. 所以△ABC的面积为![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市为拟定出台“房产限购的年龄政策”![]() 为了解人们对“房产限购年龄政策”的态度,对年龄在
为了解人们对“房产限购年龄政策”的态度,对年龄在![]() 岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下:
岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下:
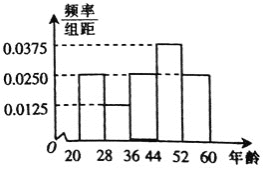
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会.现从这8人中随机抽2人.
①抽到1人是44岁以下时,求抽到的另一人是44岁以上的概率.
②记抽到44岁以上的人数为X,求随机变量X的分布列及数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
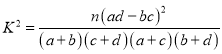 ,其中
,其中![]() .
.