题目内容
【题目】在三棱锥
各棱所在的6条直线上，互相垂直的最多有儿对？（每两条组成一对）
【答案】6
【解析】
分三步证明最多有6对互相垂直的直线.
（1）6对是可以达到的.
当
且
时，由线面垂直的性质有
，
，
.
又由三垂线定理，有
，
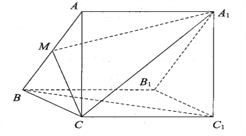
.这就得出6对互相垂直的直线(如图所示).
(2)8对是不可能的.
由于一个三角形的内角中最多有一个直角，最少有两个锐角，所以4个面三角形至少有8个锐角，又由6条直线可以组成
对直线，
知，互相垂直的直线不超过7对.
(3)7对是不可能的.
若不然，有7对垂直直线，因异面直线只有3对，故至少有4对垂直直线是共面的，
得三棱锥的4个表面都必须是直角三角形（得4对）.
进而3对成异面直线的棱也互相垂直.
此时，三棱锥的一个顶点在所对面上的射影必是该三角形的垂心，
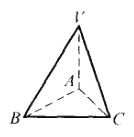
而直角三角形的垂心就是直角顶点，所以这个三棱锥的一条侧棱与底面垂直，且垂足就是垂面三角形的顶点(图中，).
这时底面三角形直角顶点的对面为锐角三角形（
为锐角三角形），与4个面均为直角三角形矛盾.
综上得，互相垂直的直线最多有6对.
练习册系列答案
阅读快车系列答案
相关题目
