[题目]已知椭圆的一个焦点坐标为．(Ⅰ)求椭圆的方程,(Ⅱ)已知点.过点的直线(与轴不重合)与椭圆交于两点.直线与直线相交于点.试证明:直线与轴平行．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆的一个焦点坐标为．

（Ⅰ）求椭圆的方程；

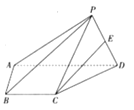
（Ⅱ）已知点，过点的直线（与轴不重合）与椭圆交于两点，直线与直线相交于点，试证明：直线与轴平行．

【答案】（Ⅰ）（Ⅱ）见解析

【解析】试题分析：（Ⅰ）由题意可知所以，即可得到求椭圆的方程；

（Ⅱ）①当直线的斜率不存在时，易证直线与轴平行

②当直线的斜率存在时，设直线的方程为 .

因为点，所以直线的方程为.

令，所以.

由消去得.显然恒成立.

所以

这时可证，即.

所以直线轴.

试题解析：

（Ⅰ）由题意可知所以.所以椭圆的方程为.

（Ⅱ）①当直线的斜率不存在时，此时轴.设，直线与轴相交于点，易得点是点和点的中点，又因为，

所以，所以直线轴.

②当直线的斜率存在时，设直线的方程为 .

因为点，所以直线的方程为.

令，所以.

由消去得.显然恒成立.

所以

因为

，

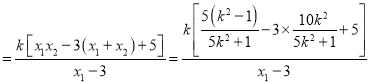
所以.

所以直线轴.

综上所述，所以直线轴.

练习册系列答案

相关题目

【题目】设函数，（）.

（1）当时，若函数与的图象在处有相同的切线，求的值；

（2）当时，若对任意和任意，总存在不相等的正实数，使得，求的最小值；

（3）当时，设函数与的图象交于两点．求证： .

【题目】已知曲线的参数方程为，其中为参数，且在直角坐标系中，以坐标原点为极点，以轴正半轴为极轴建立极坐标系.

（1）求曲线的极坐标方程；

（2）设是曲线上的一点，直线被曲线截得的弦长为，求点的极坐标.

【题目】某公司为了解用户对其产品的满意度，从A、B两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：

A地区：	62	73	81	92	95	85	74	64	53	76
	78	86	95	66	97	78	88	82	76	89
B地区：	73	83	62	51	91	46	53	73	64	82
	93	48	95	81	74	56	54	76	65	79

（Ⅰ）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度的平均值及分散程度（不要求算出具体值，给出结论即可）：

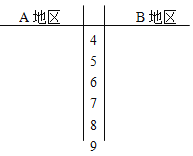
（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：

满意度评分	低于70分	70分到89分	不低于90分
满意度等级	不满意	满意	非常满意

记事件C：“A地区用户的满意度等级高于B地区用户的满意度等级”，假设两地区用户的评价结果相互独立，根据所给数据，以事件发生的频率作为相应事件发生的概率，求C的概率。

【题目】某学校高三年级共有1000名学生，其中男生650人，女生350人，为了调查学生周末的休闲方式，用分层抽样的方法抽查了200名学生.

（Ⅰ）完成下面的列联表；

	不喜欢运动	喜欢运动	合计
女生	50
男生
合计		100	200

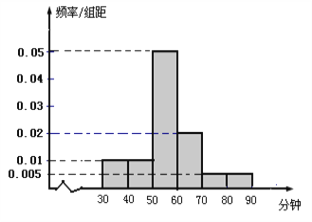
（Ⅱ）在抽取的样本中，调查喜欢运动女生的运动时间，发现她们的运动时间介于30分钟到90分钟之间，右图是测量结果的频率分布直方图，若从区间段和的所有女生中随机抽取两名女生，求她们的运动时间在同一区间段的概率.

【题目】如图，在四棱锥中，底面为梯形，平面平面

为侧棱的中点，且.

（1）证明：平面；

（2）若点到平面的距离为，且，求点到平面的距离.

【题目】已知为坐标原点，抛物线上在第一象限内的点到焦点的距离为，曲线在点处的切线交轴于点，直线经过点且垂直于轴．

（Ⅰ）求点的坐标；

（Ⅱ）设不经过点和的动直线交曲线于点和，交于点，若直线，，的斜率依次成等差数列，试问：是否过定点？请说明理由．

【题目】已知点在椭圆上，且椭圆的离心率为.

（1）求椭圆的方程；

（2）若为椭圆的右顶点，点是椭圆上不同的两点（均异于）且满足直线与斜率之积为.试判断直线是否过定点，若是，求出定点坐标，若不是，说明理由.

【题目】(2018届高三·湖南十校联考)已知函数f(x)＝x＋sin x(x∈R)，且f(y2－2y＋3)＋f(x2－4x＋1)≤0，则当y≥1时，的取值范围是(　　)

A. B.

C. [1,3－3] D.

试题分类