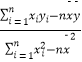题目内容
【题目】已知x∈R,符号[x]表示不超过x的最大整数,若函数f(x)=![]() (x>0),则给出以下四个结论:
(x>0),则给出以下四个结论:
①函数f(x)的值域为[0,1];
②函数f(x)的图象是一条曲线;
③函数f(x)是(0,+∞)上的减函数;
④函数g(x)=f(x)﹣a有且仅有3个零点时![]() .
.
其中正确的序号为 .
【答案】④
【解析】解:由于符号[x]表示不超过x的最大整数,函数f(x)=![]() (x>0),
(x>0),
取x=﹣1.1,则[x]=﹣2,∴f(x)=![]() >1,故①不正确.
>1,故①不正确.
由于当0<x<1,[x]=0,此时f(x)=0;
当1≤x<2,[x]=1,此时f(x)=![]() ;
;
当2≤x<3,[x]=2,此时f(x)=![]() , 此时
, 此时![]() <f(x)≤1,
<f(x)≤1,
当3≤x<4,[x]=3,此时f(x)=![]() , 此时
, 此时![]() <g(x)≤1,
<g(x)≤1,
当4≤x<5,[x]=4,此时f(x)=![]() , 此时
, 此时![]() <g(x)≤1,
<g(x)≤1,
故f(x)的图象不会是一条曲线,且 f(x)不会是(0,+∞)上的减函数,故排除②、③.
函数g(x)=f(x)﹣a有且仅有3个零点时,函数f(x)的图象和直线y=a有且仅有3个交点,
此时,![]() , 故④正确,
, 故④正确,
所以答案是:④.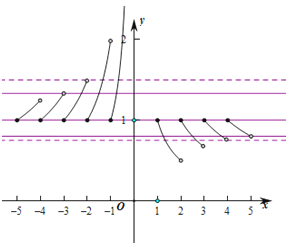

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目