题目内容
【题目】如图，若Ω是长方体ABCD﹣A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1D1 ， 则下列结论中不正确的是（ ）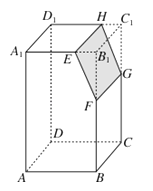
A.EH∥FG
B.四边形EFGH是矩形
C.Ω是棱柱
D.Ω是棱台
【答案】D
【解析】解：因为EH∥A1D1 ， A1D1∥B1C1 ，
所以EH∥B1C1 ， 又EH平面BCC1B1 ， 平面EFGH∩平面BCC1B1=FG，
所以EH∥平面BCB1C1 ， 又EH平面EFGH，
平面EFGH∩平面BCB1C1=FG，
所以EH∥FG，故EH∥FG∥B1C1 ，
所以选项A、C正确；
因为A1D1⊥平面ABB1A1 ，
EH∥A1D1 ， 所以EH⊥平面ABB1A1 ，
又EF平面ABB1A1 ， 故EH⊥EF，所以选项B也正确，
故选D．
根据直线与平面平行的性质定理可知EH∥FG，则EH∥FG∥B1C1 ， 从而Ω是棱柱，因为A1D1⊥平面ABB1A1 ， EH∥A1D1 ， 则EF⊥平面ABB1A1 ， 又EF平面ABB1A1 ， 故EH⊥EF，从而四边形EFGH是矩形．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
