题目内容
【题目】从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi（单位：千元）与月储蓄yi（单位：千元）的数据资料，算得 
=80， 
=20， iyi=184， 
=720．（b=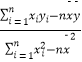 
）
（1）求家庭的月储蓄y对月收入x的线性回归方程；
（2）判断变量x与y之间是正相关还是负相关；
（3）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．
【答案】
（1）解：由题意知，n=10， 
=8， 
=2，
∴b= 
=0.3，a=2﹣0.3×8=﹣0.4，
∴y=0.3x﹣0.4．
（2）解：由于b=0.3＞0，
∴y与x之间是正相关．
（3）解：x=7时，y=0.3×7﹣0.4=1.7（千元）
【解析】（1）由题意可知n， ， ，进而代入可得b、a值，可得方程；（2）由回归方程x的系数b的正负可判断；（3）把x=7代入回归方程求其函数值即可．
练习册系列答案
特高级教师点拨系列答案
相关题目
【题目】某单位附近只有甲、乙两个临时停车场，它们各有
个车位，为了方便市民停车，某互联网停车公司对这两个停车场，在某些固定时刻的剩余停车位进行记录，如下表：
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的
，那么当车主驱车抵达单位附近时，该公司将会向车主发出停车场饱和警报.
（1）假设某车主在以上六个时刻抵达单位附近的可能性相同，求他收到甲停车场饱和警报的概率；
（2）从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率；
（3）当乙停车场发出饱和警报时，求甲停车场也发出饱和警报的概率.
