��Ŀ����
����Ŀ��Ϊ��ǿ����Ļ�����ʶ��ij������ȫ�����л���֪ʶ��������־Ը�ߣ��ӷ���������־Ը�������ѡȡ![]() ��־Ը�ߣ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���������䣨�꣩�ֳ����飺��
��־Ը�ߣ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���������䣨�꣩�ֳ����飺��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ���ֲ�����ͼ��ʾ.
���õ���Ƶ�ʷֲ�ֱ��ͼ���ֲ�����ͼ��ʾ.
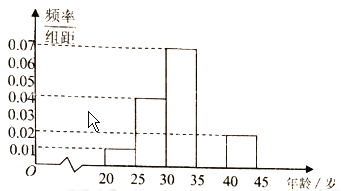
��1�����![]() ���Ƶ�ʣ�����ͼ�в���ֱ��ͼ��
���Ƶ�ʣ�����ͼ�в���ֱ��ͼ��
��2����![]() ��־Ը������ѡ���������
��־Ը������ѡ���������![]() ���־Ը��
���־Ը��![]() ��������Ҫ�����ˣ�����
��������Ҫ�����ˣ�����![]() ����Ҫ�����˵������ڲ�ͬһ��ĸ���.
����Ҫ�����˵������ڲ�ͬһ��ĸ���.
���𰸡���1����������2��![]()
�������������������1�����ʿ���Ƶ�ʷֲ�ֱ��ͼ���ر���Ҫע����������ʾ����Ƶ��/��࣬����Ƶ�ʷֲ�ֱ��ͼ��ÿ��С������������ڸ���Ƶ�ʣ�����С����������͵���1�����ǿ�������������Ƶ�ʣ�����ֱ��ͼʱ��ע��������ĸ߶ȣ���2��������Ҫ����ŵ���������⣬����Ƶ�ʷֲ�ֱ��ͼ�ɵ��������30�������Ϊ![]() �ˣ�����������
�ˣ�����������![]() ��1�ˣ���
��1�ˣ���![]() ��4�ˣ�����ת��Ϊ��5����ѡȡ3�ˣ�д�������¼��ռ䣬ȷ�������¼�������Ȼ�������3�˾���ͬһ���������Ļ����¼����������õ�3��������ͬһ��ĸ��ʣ������ݶ����¼������ص㣬���Եó������ڲ�ͬһ��ĸ���.
��4�ˣ�����ת��Ϊ��5����ѡȡ3�ˣ�д�������¼��ռ䣬ȷ�������¼�������Ȼ�������3�˾���ͬһ���������Ļ����¼����������õ�3��������ͬһ��ĸ��ʣ������ݶ����¼������ص㣬���Եó������ڲ�ͬһ��ĸ���.
�����������1����4���Ƶ��Ϊ![]() .
.
![]() , ����4���ֱ��ͼ��ͼ��ʾ��
, ����4���ֱ��ͼ��ͼ��ʾ��
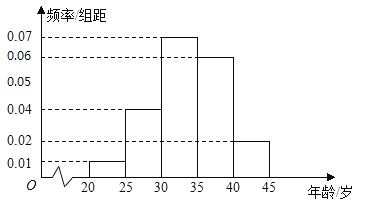
�������衰��20��־Ը������ѡ���������30���־Ը��3��������Ҫ������, ���������ͬһ�顱Ϊ�¼�A
��һ�������Ϊ![]() ��
��
�ڶ��������Ϊ![]() ��
��
���һ���־Ը��Ϊm���ڶ����4��־Ը�߷ֱ�Ϊa,b,c,d.
��m, a,b,c,d��ѡ��3��־Ը�߹���![]()
![]() 10��ѡȡ����.
10��ѡȡ����.
���ж��ڵڶ���Ĺ���![]() 4��ѡȡ����.
4��ѡȡ����.
���ԣ������¼��ĸ���Ϊ![]() .
.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�������ֻ��ķ�չ�����š�Խ��Խ��Ϊ���ǽ�����һ�ַ�ʽ.ij�����ԡ�ʹ���Ž�������̬�Ƚ��е��飬�����ȡ��50�ˣ����������Ƶ���ֲ����ԡ�ʹ���Ž��������������±�.
���䣨��λ���꣩ | [15,25�� | [25,35�� | [35,45�� | [45,55�� | [55,65�� | [65,75�� |
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
������ | 5 | 10 | 12 | 7 | 2 | 1 |
�������ԡ�����45��Ϊ�ֽ�㡱��������ͳ�������������![]() �����������ж��Ƿ���99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
�����������ж��Ƿ���99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
���䲻����45������� | �������45������� | �ϼ� | |
�� | |||
���� | |||
�ϼ� |
��������������[25,35����[55,65���ı��������а��շֲ�����ķ���ѡȡ6�˽����ٵ��飬����������3�ˡ��������������3����������1��������[55,65���ĸ���.
�ο��������£�
���ٽ�ֵ����
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() �Ĺ۲�ֵ��
�Ĺ۲�ֵ�� ![]() ������
������![]() ��
��