题目内容
【题目】已知曲线
在
处的切线方程为
．
（1）求
的值；
（2）若对任意
恒成立，求
的取值范围．
【答案】（1）
,
；（2）
．
【解析】
试题分析：（1）由题意得
，又
；（2）由（1）知
对任意
恒成立
，对任意
恒成立
．又不等式整理可得
，令
, 在利用导数工具得
的取值范围是．
试题解析： （1）由题意得，因曲线
在
处的切线方程为
，
所以，得，即，又，从而．．．．．．．．．．．．．．．．．．．4分
（2）由（1）知对任意恒成立，
所以，即，对任意恒成立，从而．．．．．．．．．6分
又不等式整理可得，令，
所以
，令
得
，．．．．．．．．．．．．9分
当
时，
，函数
在
上单调递增，
同理，函数
在
上单调递减，所以，．．．．．．．．．．．．11分
综上所述，实数的取值范围是．．．．．．．．．．．．．．．．．．．．．．．．12分
寒假大串联黄山书社系列答案
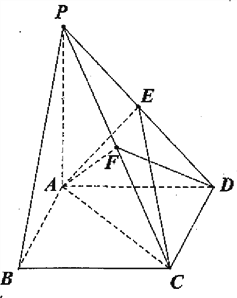
寒假创新型自主学习第三学期寒假衔接系列答案
【题目】如图，四棱锥P—ABCD的底面ABCD为矩形，PA⊥平面ABCD，点E是棱PD的中点，点F是PC的中点．
（Ⅰ）证明：PB∥平面AEC；
（Ⅱ）若底面ABCD为正方形，
，求二面角C—AF—D大小．
【题目】为了对2016年某校中考成绩进行分析，在60分以上的全体同学中随机抽出8位，他们的数学分数（已折算为百分制）从小到大排是60、65、70、75、80、85、90、95，物理分数从小到大排是72、77、80、84、88、90、93、95．
（1）若规定85分（包括85分）以上为优秀，求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率；
（2）若这8位同学的数学、物理、化学分数事实上对应如下表：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
化学分数 | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
①用变量
与
与
的相关系数说明物理与数学、化学与数学的相关程度；
②求与与的线性回归方程（系数精确到0.01），当某同学的数学成绩为50分时，估计其物理、化学两科的得分．
参考公式：相关系数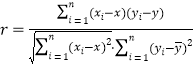
，
回归直线方程是：
，其中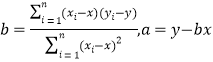
，
参考数据：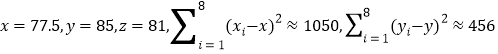
，
，
，
．