题目内容
【题目】已知f(x)是R上的奇函数，当x＞0时，解析式为f(x)＝
.
(1)求f(x)在R上的解析式；
(2)用定义证明f(x)在(0，＋∞)上为减函数．
【答案】(1) f(x)＝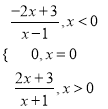
(2)见解析
【解析】试题分析：（1）分别求出当x＜0和x=0时的解析式，写成分段函数的形式；（2）设x1，x2∈(0，＋∞)，且x1＜x2，通过作差证明f(x1)＞f(x2)即可。
试题解析：(1)设x＜0，则－x＞0，
∴f(－x)＝
.
又∵f(x)是R上的奇函数，
∴f(－x)＝－f(x)＝，
∴f(x)＝
.
又∵奇函数在x=0时有意义，
∴f(0)＝0，
∴函数的解析式为f(x)＝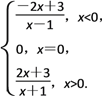
(2)证明：设x1，x2∈(0，＋∞)，且x1＜x2，
则f(x1)－f(x2)＝
－
＝
＝
.
∵x1，x2∈(0，＋∞)，x1＜x2，
∴x1＋1＞0，x2＋1＞0，x2－x1＞0，
∴f(x1)－f(x2)＞0，
∴f(x1)＞f(x2)，
∴函数f(x)在(0，＋∞)上为减函数．
新课标快乐提优暑假作业陕西旅游出版社系列答案
【题目】一企业从某条生产线上随机抽取100件产品，测量这些产品的某项技术指标值x，得到如下的频率分布表：
x | [11，13） | [13，15） | [15，17） | [17，19） | [19，21） | [21，23） |
频数 | 2 | 12 | 34 | 38 | 10 | 4 |
（Ⅰ）作出样本的频率分布直方图，并估计该技术指标值x的平均数和众数；
（Ⅱ）若x＜13或x≥21，则该产品不合格．现从不合格的产品中随机抽取2件，求抽取的2件产品中技术指标值小于13的产品恰有一件的概率．
【题目】沪昆高速铁路全线2016年12月28日开通运营．途经鹰潭北站的
、
两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了月乘车次数的频率分布直方图和频数分布表．
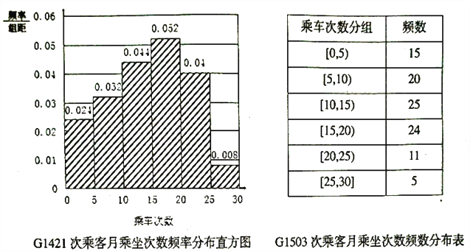
（1）若将频率视为概率，月乘车次数不低于15次的称之为“老乘客”，试问：哪一车次的“老乘客”较多，简要说明理由；
（2）已知在次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成
列联表，并根据资料判断，是否有
的把握认为年龄与乘车次数有关，说明理由．
老乘客 | 新乘客 | 合计 | |
50岁以上 | |||
50岁以下 | |||
合计 |
附：随机变量
（其中
为样本容量）
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
