Question

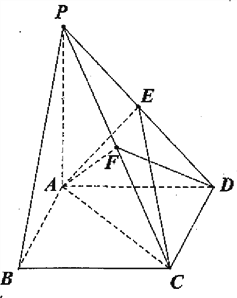
【题目】如图，四棱锥P—ABCD的底面ABCD为矩形，PA⊥平面ABCD，点E是棱PD的中点，点F是PC的中点．

（Ⅰ）证明：PB∥平面AEC；

（Ⅱ）若底面ABCD为正方形，，求二面角C—AF—D大小．

Answer 1

【答案】(1)详见解析;(2)60°.

【解析】试题分析：(1)要证线面平行，即证线线平行；（2）建立空间直角坐标系，

试题解析：

（Ⅰ）连接BD，设AC∩BD＝O，连结OE，

∵四边形ABCD为矩形，∴O是BD的中点，

∵点E是棱PD的中点，∴PB∥EO，

又PB平面AEC，EO平面AEC，

∴PB∥平面AEC．

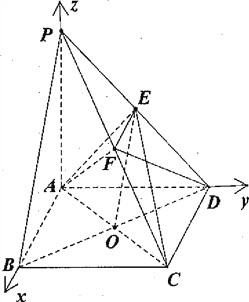
（Ⅱ）由题可知AB，AD，AP两两垂直，则分别以、、的方向为坐标轴方向建立空间直角坐标系．明确平面DAF的一个法向量为，利用二面角公式求角.

设由可得AP＝AB，

于是可令AP＝AB＝AD＝2，则

A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），P（0，0，2），E（0，1，1），F（1，1，1）

设平面CAF的一个法向量为．由于，

所以，解得x＝－1，所以．

因为y轴平面DAF，所以可设平面DAF的一个法向量为．

由于，所以，解得z＝－1，

所以．

故．所以二面角C—AF—D的大小为60°．