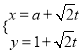题目内容
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
【答案】(Ⅰ)见解析;(2)2.
【解析】试题分析: (1)根据已知条件求出![]() ,设
,设![]() .根据
.根据![]() 得出
得出![]() 在
在![]() 上为增函数,即可得证.
上为增函数,即可得证.
(2)令![]() ,则
,则![]() 只能取
只能取![]() 或
或![]() .当
.当![]() 时,设
时,设![]() ,求出
,求出![]() .由
.由![]() 得
得![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 是增函数,即
是增函数,即![]() .故
.故![]() 对一切
对一切![]() 恒成立.
恒成立.
试题解析:(Ⅰ)当![]() 时,
时,![]() ,则
,则![]()
令![]() ,则
,则![]()
令![]() ,得
,得![]() ,故
,故![]() 在
在![]() 时取得最小值
时取得最小值
∵![]() ,∴
,∴![]() 在
在![]() 上为增函数.
上为增函数.
∴![]() .
.
(Ⅱ)![]() ,
,
由![]() ,得
,得![]() 对一切
对一切![]() 恒成立
恒成立
当![]() 时,可得
时,可得![]() ,所以若存在,则正整数
,所以若存在,则正整数![]() 的值只能取1,2
的值只能取1,2
下面证明当![]() 时,不等式恒成立
时,不等式恒成立
设![]() ,则
,则![]()
由(Ⅰ)![]() ∴
∴![]()
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
即![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数
∴![]()
当![]() 时,不等式恒成立
时,不等式恒成立
所以![]() 的最大值是22.
的最大值是22.

练习册系列答案
相关题目