题目内容
11. 某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.(I)请说明A公司应选择哪个网站;
(Ⅱ)现将抽取的样本分布近似看作总体分布,A公司根据所选网站的日访问量n进行付费,其付费标准如下:
| 选定网站的日访问量n(单位:万次) | A公司的付费标准(单位:元/日) |
| n<25 | 500 |
| 25≤n≤35 | 700 |
| n>35 | 1000 |
分析 (I)根据茎叶图中的数据,计算甲、乙二人的平均数与方差,由此判断A公司应选择的网站;
(Ⅱ)根据茎叶图计算乙网站的日访问量对应的概率,利用表中数据计算公司每月应支付的费用.
解答 解:(I)根据茎叶图,得;
$\overline{{x}_{甲}}$=(15+24+28+25+30+36+30+32+35+45)÷10=30,
${{s}_{甲}}^{2}$=$\frac{1}{10}$[(15-30)2+(24-30)2+(28-30)2+(25-30)2+(30-30)2
+(36-30)2+(30-30)2+(32-30)2+(35-30)2+(45-30)2]=58;
$\overline{{x}_{乙}}$=(18+25+22+24+32+38+30+36+35+40)÷10=30,
${{x}_{乙}}^{2}$=$\frac{1}{10}$[(18-30)2+(25-30)2+(22-30)2+(24-30)2+(32-30)2
+(38-30)2+(30-30)2+(36-30)2+(35-30)2+(40-30)2]=49.8;
∵$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${{s}_{甲}}^{2}$>${{s}_{乙}}^{2}$,
∴A公司应选择乙网站;
(Ⅱ)由(Ⅰ)得A公司应选择乙网站,
根据题意得,乙网站日访问量n<25的概率为0.3,
日访问量25≤n≤35的概率为0.4,
日访问量n>35的概率为0.3,
∴A公司每月应付给乙网站的费用为
S=30×(00×0.3+700×0.4+1000×0.3)=21900元.
点评 本题考查了求平均数与方差的应用问题,也考查了统计数表的应用问题,是基础题目.

练习册系列答案
相关题目
1.已知命题p:?x0∈R,x02+2x0+1≤0,则¬p为( )
| A. | ?x0∈R,x02+2x0+1>0 | B. | ?x∈R,x2+2x+1≤0 | ||
| C. | ?x∈R,x2+2x+1≥0 | D. | ?x∈R,x2+2x+1>0 |
2.设集合A={x∈N|y=ln(2-x)},B={x|x(x-1)≤0},则A∩B=( )
| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {1} | D. | {0,1} |
19.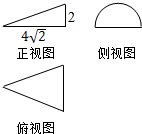 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{8\sqrt{2}π}{3}$ | B. | $\frac{16\sqrt{2}π}{3}$ | C. | 4$\sqrt{2}π$ | D. | 8$\sqrt{2}π$ |
20.已知集合 A={x∈R|x-1≥0},B={x∈R||x|≤2},则A∩B=( )
| A. | {x∈R|-2≤x≤2} | B. | {x∈R|-1≤x≤2} | C. | {x∈R|1≤x≤2} | D. | {x∈R|-1≤x≤1} |
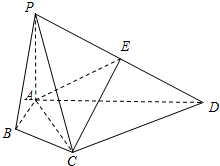 在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.
在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.