题目内容
【题目】设![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求![]() 的值;
的值;
(2)若对于任意的![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)求证: ![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)详见解析
(Ⅲ)详见解析
【解析】试题分析:(Ⅰ)先求导数,再根据导数几何意义列方程,解方程可得![]() 的值;(Ⅱ)不等式恒成立问题,一般转化为对应函数最值问题,本题去分母转化为差函数:
的值;(Ⅱ)不等式恒成立问题,一般转化为对应函数最值问题,本题去分母转化为差函数: ![]() ,因为
,因为![]() ,所以
,所以![]() 最大值不小于
最大值不小于![]() ,根据
,根据![]() 导函数符号可得
导函数符号可得![]() 才满足条件.(Ⅲ)不等式证明中涉及求和问题,一般方法为适当放缩,再利用裂项相消法给予证明.本题由(Ⅱ)知,当
才满足条件.(Ⅲ)不等式证明中涉及求和问题,一般方法为适当放缩,再利用裂项相消法给予证明.本题由(Ⅱ)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立,所以放缩这一难点已暗示,下面只需令
成立,所以放缩这一难点已暗示,下面只需令![]() 得
得![]() ,即
,即![]() ,最后叠加可得证.
,最后叠加可得证.
试题解析:(Ⅰ) 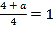
由题设![]() ,∴
,∴![]()
![]() .
.
(Ⅱ)![]() ,
,![]() ,
, ![]() ,即
,即![]()
设![]() ,即
,即![]() .
.
![]()
![]()
①若![]() ,
, ![]() ,这与题设
,这与题设![]() 矛盾
矛盾
②若![]() 当
当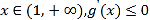 ,
, ![]() 单调递增,
单调递增, ![]() ,与题设矛盾.
,与题设矛盾.
③若![]() 当
当![]() ,
, ![]() 单调递减,
单调递减, ![]() ,即不等式成立
,即不等式成立
综上所述, ![]() .
.
(Ⅲ)由(Ⅱ)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立.
成立.
不妨令![]() 所以
所以![]() ,
,
![]()
![]()
![]()
…………
![]()
累加可得
∴![]()

练习册系列答案
相关题目