题目内容
【题目】若函数f(x)=ax2-(3a-1)x+a2在[1,+∞)上是增函数,求实数a的取值范围.
【答案】0≤a≤1.
【解析】试题分析:先讨论参数a是否为0,若a=0,代入可得一次函数是增函数,成立;若a≠0,则二次函数开口向上,且x=1在对称轴的右侧,列出不等式解出a的范围即可.
试题解析:
①a=0时,f(x)=x在[1,+∞)上是增函数.
②a≠0时,∵f(x)在[1,+∞)上是增函数.
∴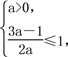 解得0<a≤1.
解得0<a≤1.
综上0≤a≤1.
点睛:本题考查一次函数和二次函数的单调性,属于基础题.根据函数解析式的形式,先要对最高次项的系数进行讨论,当a=0时,函数为一次函数,将a=0代入可知一次项系数为正,故为增函数;当a≠0时,函数为二次函数,若要使函数在[1,+∞)上是增函数,则需要开口向上,且[1,+∞)为增区间的子集,比较对称轴和1的大小关系列出不等式求解即可.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目

