题目内容
【题目】平面直角坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的![]() 倍和
倍和![]() 倍后,得到曲线
倍后,得到曲线![]()
(1)试写出曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求点
上求点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.
【答案】(1) ![]() 的参数方程为
的参数方程为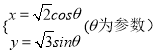 ; (2)
; (2) ![]() ,此时
,此时![]() 点的坐标为
点的坐标为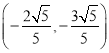 .
.
【解析】试题分析:(1)写出曲线![]() 的参数方程,先求出曲线
的参数方程,先求出曲线![]() 的参数方程为
的参数方程为![]() ,设
,设![]() ,由已知将曲线
,由已知将曲线![]() 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的![]() 倍和
倍和![]() 倍后,可得
倍后,可得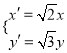 ,代换即可求出曲线
,代换即可求出曲线![]() 的参数方程.(2)在曲线
的参数方程.(2)在曲线![]() 上求点
上求点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最大,并求距离最大值,由(1)得点
的距离最大,并求距离最大值,由(1)得点![]() ,利用点到直线距离公式,建立关于
,利用点到直线距离公式,建立关于![]() 的三角函数式求解.
的三角函数式求解.
试题解析:(1)曲线![]() 的参数方程为
的参数方程为![]() 1分
1分
由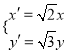 得
得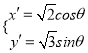 3分
3分
![]()
![]() 的参数方程为
的参数方程为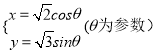 5分
5分
(2)由(1)得点![]()
点![]() 到直线
到直线![]() 的距离
的距离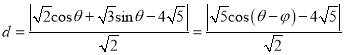
![]() 7分
7分
![]() 9分
9分
此时![]() 点的坐标为
点的坐标为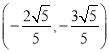 10分
10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知随机变量![]() 的取值为不大于
的取值为不大于![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中![]() (
(![]() )满足:
)满足: ![]() ,且
,且![]() .
.
定义由![]() 生成的函数
生成的函数![]() ,令
,令![]() .
.
(I)若由![]() 生成的函数
生成的函数![]() ,求
,求![]() 的值;
的值;
(II)求证:随机变量![]() 的数学期望
的数学期望![]() ,
, ![]() 的方差
的方差![]() ;
;
(![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由![]() 生成的函数记为
生成的函数记为![]() ,求
,求![]() 的值.
的值.