题目内容
13.已知A为椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的一个动点,直线AB,AC分别过焦点,F1,F2,且与椭圆交于B,C两点,若当AC⊥x轴时,恰好有|AF1|:|AF2|=3:1,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{3}$ |
分析 由椭圆方程求出|AF2|的长,结合椭圆定义求得|AF1|,再由|AF1|:|AF2|=3:1列式求得椭圆的离心率.
解答 解:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点横坐标为c,不妨设A为椭圆在第一象限的点,
当AC⊥x轴时,由$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),得yA=$\frac{{b}^{2}}{a}$.
即|AF2|=$\frac{{b}^{2}}{a}$,由椭圆定义得,|AF1|=2a-$\frac{{b}^{2}}{a}$,
又|AF1|:|AF2|=3:1,得$\frac{2a-\frac{{b}^{2}}{a}}{\frac{{b}^{2}}{a}}$=3,即a2=2b2=2(a2-c2),
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
故选:A.
点评 本题考查了椭圆的简单几何性质,考查了椭圆的定义,是基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
18.已知点P在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,F1F2分别是其左、右焦点,若|PF1|=2|PF2|,则该椭圆的离心率的取值范围是( )
| A. | (0,$\frac{1}{3}$] | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{1}{3}$) | D. | [$\frac{1}{3}$,1) |
5.已知椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的一个焦点为(2,0),则椭圆的短轴长为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 4$\sqrt{3}$ |
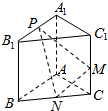 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$.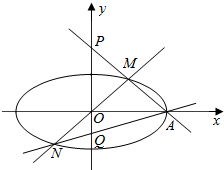 在平面直角坐标系xOy中,已知椭圆C的右顶点为A,两焦点坐标分别为(-$\sqrt{3}$,0)和($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).过点O的直线交椭圆C于M、N两点,直线AM、AN分别交y轴于P、Q两点.
在平面直角坐标系xOy中,已知椭圆C的右顶点为A,两焦点坐标分别为(-$\sqrt{3}$,0)和($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).过点O的直线交椭圆C于M、N两点,直线AM、AN分别交y轴于P、Q两点.