题目内容
4.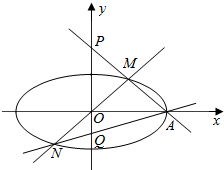 在平面直角坐标系xOy中,已知椭圆C的右顶点为A,两焦点坐标分别为(-$\sqrt{3}$,0)和($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).过点O的直线交椭圆C于M、N两点,直线AM、AN分别交y轴于P、Q两点.
在平面直角坐标系xOy中,已知椭圆C的右顶点为A,两焦点坐标分别为(-$\sqrt{3}$,0)和($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).过点O的直线交椭圆C于M、N两点,直线AM、AN分别交y轴于P、Q两点.(1)求椭圆C的标准方程;
(2)若$\overrightarrow{PM}$=λ$\overrightarrow{MA}$,且$\overrightarrow{MN}$⊥$\overrightarrow{MA}$,求实数λ的值;
(3)以线段PQ为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
分析 (1)通过椭圆的性质计算可得结论;
(2)设M(x0,y0),通过$\overrightarrow{MN}$⊥$\overrightarrow{MA}$可得${x}_{0}=\frac{2}{3}$,利用$\overrightarrow{PM}$=λ$\overrightarrow{MA}$计算可得结论;
(3)设M(x0,y0),通过令直线MA、AN中x=0可得P、Q点坐标,进而可得以直线PQ为直径的圆的方程,计算可得结论.
解答 解:(1)设椭圆C的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
依题意可知:2a=PF1+PF2=$\sqrt{12+\frac{1}{4}}$+$\sqrt{\frac{1}{4}}$=4,即a=2,
又∵c=$\sqrt{3}$,∴b2=a2-c2=1,
∴椭圆C的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)设M(x0,y0),
∵$\overrightarrow{MN}$⊥$\overrightarrow{MA}$,∴(x0,y0)•(2-x0,-y0)=0,
即$2{x}_{0}-{{x}_{0}}^{2}-{{y}_{0}}^{2}=0$,
又$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}=1$,∴${x}_{0}=\frac{2}{3}$或x0=2(舍),
∵$\overrightarrow{PM}$=λ$\overrightarrow{MA}$,∴$\frac{2}{3}$=λ(2-$\frac{2}{3}$),
∴λ=$\frac{1}{2}$;
(3)结论:以线段PQ为直径的圆过定点(-1,0)和(1,0).
理由如下:
设M(x0,y0),直线MA:y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),
令x=0,得y=$\frac{-2{y}_{0}}{{x}_{0}-2}$=$\frac{2{y}_{0}}{2-{x}_{0}}$,即P(0,$\frac{2{y}_{0}}{2-{x}_{0}}$),
同理可得:Q(0,-$\frac{2{y}_{0}}{{2+x}_{0}}$),
∴以直线PQ为直径的圆的方程为:x2+(y-$\frac{2{y}_{0}}{2-{x}_{0}}$)(y+$\frac{2{y}_{0}}{{2+x}_{0}}$)=0,
令y=0得:x2=$\frac{2{y}_{0}}{2-{x}_{0}}$•$\frac{2{y}_{0}}{{2+x}_{0}}$=$\frac{4{{y}_{0}}^{2}}{4-{{x}_{0}}^{2}}$,
又∵$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}=1$,即4${{y}_{0}}^{2}$=4-${{x}_{0}}^{2}$,
∴x2=1,即x=±1.
∴以线段PQ为直径的圆过定点(-1,0)和(1,0).
点评 本题是一道直线与圆锥曲线的综合题,涉及到圆的方程、向量数量积运算等基础知识,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | $\frac{7π}{6}$ | D. | $\frac{π}{3}$ |
| A. | $\frac{{3-\sqrt{5}}}{2}$ | B. | $\frac{{3+\sqrt{5}}}{8}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{1+\sqrt{5}}}{8}$ |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{3}$ |