题目内容
已知函数f(x)= ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.

(1)求函数y=f(x)的解析式;
(2)若g(x)= -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.
 ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.
(1)求函数y=f(x)的解析式;
(2)若g(x)=
 -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.(1)f(x)= x3-x+3
x3-x+3
(2)[1,+∞)
 x3-x+3
x3-x+3(2)[1,+∞)
(1)∵f′(x)=ax2+a-2,
由图可知函数f(x)的图象过点(0,3),且f′(1)=0.
得 即
即
∴f(x)= x3-x+3.
x3-x+3.
(2)∵g(x)= -2ln x=kx-
-2ln x=kx- -2ln x,
-2ln x,
∴g′(x)=k+ -
- =
= .
.
∵函数y=g(x)的定义域为(0,+∞),
∴若函数y=g(x)在其定义域内为单调增函数,则函数g′(x)≥0在(0,+∞)上恒成立,即kx2+k-2x≥0在区间(0,+∞)上恒成立.
即k≥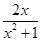 在区间(0,+∞)上恒成立.
在区间(0,+∞)上恒成立.
令h(x)=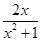 ,x∈(0,+∞),
,x∈(0,+∞),
则h(x)=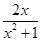 =
= ≤1(当且仅当x=1时取等号).
≤1(当且仅当x=1时取等号).
∴k≥1.
∴实数k的取值范围是[1,+∞).
由图可知函数f(x)的图象过点(0,3),且f′(1)=0.
得
 即
即
∴f(x)=
 x3-x+3.
x3-x+3.(2)∵g(x)=
 -2ln x=kx-
-2ln x=kx- -2ln x,
-2ln x,∴g′(x)=k+
 -
- =
= .
.∵函数y=g(x)的定义域为(0,+∞),
∴若函数y=g(x)在其定义域内为单调增函数,则函数g′(x)≥0在(0,+∞)上恒成立,即kx2+k-2x≥0在区间(0,+∞)上恒成立.
即k≥
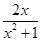 在区间(0,+∞)上恒成立.
在区间(0,+∞)上恒成立.令h(x)=
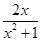 ,x∈(0,+∞),
,x∈(0,+∞),则h(x)=
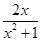 =
= ≤1(当且仅当x=1时取等号).
≤1(当且仅当x=1时取等号).∴k≥1.
∴实数k的取值范围是[1,+∞).

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
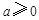 ,
, .
.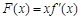 ,讨论
,讨论 在
在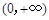 内的单调性并求极值;
内的单调性并求极值;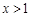 时,恒有
时,恒有 .
.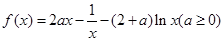
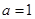 时,求
时,求 的极值;
的极值; 时,讨论
时,讨论 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. ,求F(x)=f(x)-g(x)的单调区间;
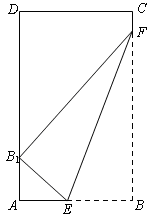
,求F(x)=f(x)-g(x)的单调区间; ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为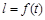 .
. 
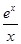 ,f(2)=
,f(2)=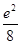 ,则x>0时,f(x)( )
,则x>0时,f(x)( ) 在
在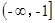 上递增,则
上递增,则 的范围是( )
的范围是( )

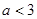

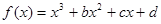 在区间
在区间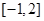 上是减函数,那么
上是减函数,那么 的最大值为 .
的最大值为 . ,函数
,函数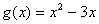 ,它们的定义域均为
,它们的定义域均为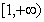 ,并且函数
,并且函数 的图像始终在函数
的图像始终在函数 的上方,那么
的上方,那么 的取值范围是( )
的取值范围是( )