题目内容
3.在正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线有无数条.分析 先画出正方体,然后根据题意试画与三条直线A1D1,EF,CD都相交的直线,从而发现结论.
解答 解:在EF上任意取一点M,如图: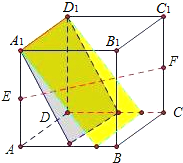
直线A1D1与M确定一个平面,
这个平面与CD有且仅有1个交点N,
当M取不同的位置就确定不同的平面,
从而与CD有不同的交点N,
而直线MN与这3条异面直线都有交点.
故在空间中与三条直线A1D1,EF,CD都相交的直线有无数条,
故答案为:无数
点评 本题主要考查立体几何中空间直线相交问题,同时考查学生的空间想象能力.

练习册系列答案
相关题目
13.有一个圆心为(a,b),半径为c的定圆如图所示,则直线ax-by+c=0与直线x+y-1=0的交点在( )


| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |