Question

【题目】已知函数的图象如图所示，则的取值范围是( )

A. B. C. D.

Answer 1

【答案】D

【解析】由图象可知：经过原点,∴f(0)=0=d，

∴.

由图象可得：函数f(x)在[1,1]上单调递减,函数f(x)在x=1处取得极大值。

∴f′(x)=3ax2+2bx+c0在[1,1]上恒成立,且f′(1)=0.

得到3a2b+c=0，即c=2b3a，

∵f′(1)=3a+2b+c<0，

∴4b<0，即b<0，

∵f′(2)=12a+4b+c>0，

∴3a+2b>0，

设k=,则k=，

建立如图所示的坐标系,则点A(1,2)，

则k=式中变量a、b满足下列条件，

作出可行域如图：

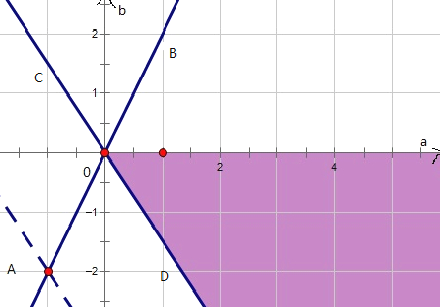
∴k的最大值就是kAB=,k的最小值就是kCD,而kCD就是直线3a+2b=0的斜率,kCD=，

∴<k<.

∴故选D.