题目内容
【题目】在四棱锥![]() 中,
中, ![]() 为正三角形,四边形
为正三角形,四边形![]() 为矩形,平面
为矩形,平面![]()
![]() 平面
平面![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点。
的中点。
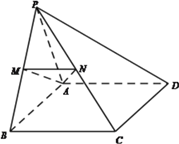
(Ⅰ)求证: ![]() //平面
//平面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:(Ⅰ)MN是△ABC的中位线,可得MN∥BC∥AD,即可证以MN∥平面PAD.
(Ⅱ)过点P作PO垂直于AB,交AB于点O,因为平面PAB⊥平面ABCD,所以PO⊥平面ABCD,如图建立空间直角坐标系设AB=2,则A(-1,0,0),C(1,1,0),M(![]() ,0,
,0, ![]() ),B(1,0,0),N(
),B(1,0,0),N(![]() ,
,![]() ,
, ![]() ),利用向量法求解.
),利用向量法求解.
试题解析:
(Ⅰ)证明:∵M,N分别是PB,PC中点
∴MN是△ABC的中位线 ∴MN∥BC∥AD
又∵AD平面PAD,MN![]() 平面PAD
平面PAD
所以MN∥平面PAD.
(Ⅱ)过点P作PO垂直于AB,交AB于点O,
因为平面PAB⊥平面ABCD,所以PO⊥平面ABCD,
如图建立空间直角坐标系

设AB=2,则A(-1,0,0),C(1,1,0),M(![]() ,0,
,0, ![]() ),
),
B(1,0,0),N(![]() ,
,![]() ,
, ![]() ),则
),则![]() ,
, 
设平面CAM法向量为![]() ,由
,由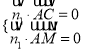 可得
可得
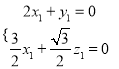 ,令
,令![]() ,则
,则![]() ,即
,即![]()
平面![]() 法向量
法向量![]()
所以,二面角![]() 的余弦值
的余弦值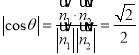
因为二面角![]() 是锐二面角,
是锐二面角,
所以二面角![]() 等于
等于![]()

【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1) 根据题意完成表格;
(2) 是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
参考公式及数据: 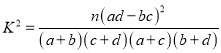 ,其中
,其中![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.