题目内容
【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动，在每一轮活动中，依次播放三首乐曲，然后甲猜第一首，乙猜第二首，丙猜第三首，若有一人猜错，则活动立即结束；若三人均猜对，则该小组进入下一轮，该小组最多参加三轮活动．已知每一轮甲猜对歌名的概率是
，乙猜对歌名的概率是
，丙猜对歌名的概率是
，甲、乙、丙猜对与否互不影响．
(I)求该小组未能进入第二轮的概率；
(Ⅱ)记乙猜歌曲的次数为随机变量
，求
的分布列和数学期望．
【答案】（Ⅰ）
；
（Ⅱ）
的分别列为
.
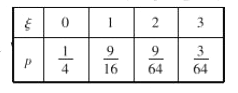
【解析】试题分析：（1）分别将甲、乙、丙第
次猜对歌名记为事件
， 
， 
，则
， 
， 
相互独立.该小组未能进入第二轮的概率
（2）利用相互独立事件的概率计算公式、对立事件的概率计算公式即可得出．
试题解析：
分别将甲、乙、丙第
次猜对歌名记为事件
， 
， 
，则
， 
， 
相互独立.
（Ⅰ）该小组未能进入第二轮的概率
.
（Ⅱ）乙猜对歌曲次数
的可能取值为0,1,2,3，
，
，
，
，
，
，
∴
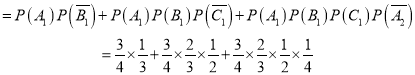
的分别列为
.
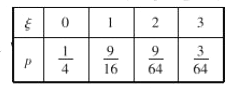
练习册系列答案
相关题目
