题目内容
【题目】如图,梯形ABCD所在的平面与等腰梯形ABEF所在的平面互相垂直,AB∥CD∥EF,AB⊥AD,CD=DA=AF=FE=2,AB=4.
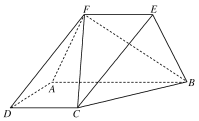
(1)求证:DF∥平面BCE;
(2)求二面角C—BF—A的正弦值;
(3)线段CE上是否存在点G,使得AG⊥平面BCF?请说明理由.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由CD∥EF, CD=EF,得到四边形CDFE为平行四边形,从而DF∥CE,由线面平行的判定定理得证DF∥平面BCE;(2)在平面ABEF内,过A作AZ⊥AB,以A为原点,AD、AB、AZ所在直线分别为x轴,y轴,z轴建立空间直角坐标系,写出相应的坐标,求出平面BCF的一个法向量n和平面ABF的一个法向量v的坐标,利用夹角公式求出二面角C—BF—A的余弦值,进而用同角三角函数关系求出正弦值;(3)假设存在满足条件的点G,设![]() =λ
=λ![]() ,求出G点坐标,从而得
,求出G点坐标,从而得![]() 的坐标,由
的坐标,由![]() ∥n构造方程组,方程组无解,从而判断满足条件的点G不存在.
∥n构造方程组,方程组无解,从而判断满足条件的点G不存在.
(1)证明:因为CD∥EF,且CD=EF,所以四边形CDFE为平行四边形,所以DF∥CE,因为DF平面BCE,
所以DF∥平面BCE.
(2)在平面ABEF内,过A作AZ⊥AB,因为平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,又AZ平面ABEF,AZ⊥AB,所以Az⊥平面ABCD,
所以AD⊥AB,AD⊥AZ,AZ⊥AB,
如图建立空间直角坐标系A—xyz.
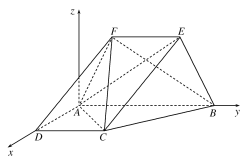
由题意得,A(0,0,0),B(0,4,0),C(2,2,0),E(0,3,![]() ),F(0,1,
),F(0,1,![]() ).
).
所以![]() =(2,-2,0),
=(2,-2,0),![]() =(0,-3,
=(0,-3,![]() ).
).
设平面BCF的法向量为n=(x,y,z),则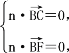 即
即![]()
令y=1,则x=1,z=![]() ,所以n=(1,1,
,所以n=(1,1,![]() ).
).
平面ABF的一个法向量为v=(1,0,0),
则cos〈n,v〉=![]() =
=![]() ,sin〈n,v〉=
,sin〈n,v〉=![]() .
.
所以二面角C—BF—A的正弦值为![]() .
.
(3)线段CE上不存在点G,使得AG⊥平面BCF,理由如下:
假设线段CE上存在点G,使得AG⊥平面BCF,设![]() =λ
=λ![]() ,其中λ∈[0,1].
,其中λ∈[0,1].
设G(x2,y2,z2),则有(x2-2,y2-2,z2)=(-2λ,λ,![]() λ),
λ),
所以x2=2-2λ,y2=2+λ,z2=![]() λ,从而G(2-2λ,2+λ,
λ,从而G(2-2λ,2+λ,![]() λ),
λ),
所以![]() =(2-2λ,2+λ,
=(2-2λ,2+λ,![]() λ).
λ).
因为AG⊥平面BCF,所以![]() ∥n.
∥n.
所以有![]() =
=![]() =
=![]() ,
,
因为上述方程无解,所以假设不成立.
所以线段CE上不存在点G,使得AG⊥平面BCF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解儿子身高与其父亲身高的关系,随机调查了5对父子的身高,统计数据如下表所示.
编 号 | A | B | C | D | E |
父亲身高 | 174 | 176 | 176 | 176 | 178 |
儿子身高 | 175 | 175 | 176 | 177 | 177 |
(1)从这五对父子任意选取两对,用编号表示出所有可能取得的结果,并求随机事件![]() “两对父子中儿子的身高都不低于父亲的身高”发生的概率;
“两对父子中儿子的身高都不低于父亲的身高”发生的概率;
(2)由表中数据,利用“最小二乘法”求![]() 关于
关于![]() 的回归直线的方程.
的回归直线的方程.
参考公式: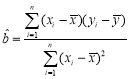 ,
,![]() ;回归直线:
;回归直线:![]() .
.