Question

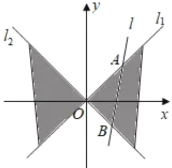
【题目】如图，在平面直角坐标系中，直线与直线之间的阴影部分记为，区域中动点到的距离之积为1.

（1）求点的轨迹的方程；

（2）对于区域中动点，求的取值范围；

（3）动直线穿过区域，分别交直线于两点，若直线与点的轨迹有且只有一个公共点，求证：的面积值为定值.

Answer 1

【答案】（1）；（2）；（3）证明见解析

【解析】

（1）根据点到直线的距离关系建立方程即可求出点的轨迹方程；

（2）将 变形为，利用其几何意义求范围即可；
（3）根据直线和双曲线的位置关系，结合三角形的面积公式进行求解即可．

解：（1）由题意得，即 ．
因为点在区域内，所以与同号，得，
即点的轨迹的方程为；

（2），

的几何意义为：区域中动点到点的距离的平方再减去5.

观察图形得，区域中动点到点的距离的最小值就是点到直线的距离，无最大值，

即的最小值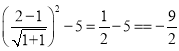为，

的取值范围为；
（3）设直线与轴相交于点，

当直线的斜率不存在时，

，，得．
当直线的斜率存在时，

设其方程为，显然，则，
把直线的方程与:联立

得，
由直线与轨迹C有且只有一个公共点，

知，
，

或．
设，

由得，

同理，得．
．
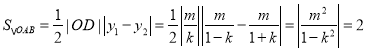综上，的面积恒为定值2．