题目内容
18.已知命题p:函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+x在R上无极值,q:函数f(x)=x3-3x-a在(0,2)上两个不等的零点,若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
分析 命题p为真时,求f′(x)=x2-ax+1,f(x)在R上无极值,从而△≤0,从而可得到-2≤a≤2;命题q为真时,求f′(x)=3(x2-1),f(x)在(0,2)上有两个不等零点,从而得到$\left\{\begin{array}{l}{f(0)>0}\\{f(1)<0}\\{f(2)>0}\end{array}\right.$,这样可求得0<a<2.根据条件可知p真q假,或p假q真,分别求出这两种情况下a的取值范围再求并集即可.
解答 解:命题p:f′(x)=x2-ax+1,则:f′(x)≥0在R上恒成立;
∴△=a2-4≤0;
∴-2≤a≤2;
命题q:f′(x)=3(x2-1);
∴函数f(x)在(0,1)上单调递减,在(1,2)上单调递增,∴根据条件可画出f(x)在(0,2)上的图象如下: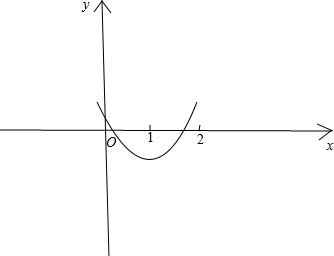 由图象可知:
由图象可知:
$\left\{\begin{array}{l}{f(0)=-a>0}\\{f(1)=-2-a<0}\\{f(2)=2-a>0}\end{array}\right.$;
解得-2<a<0;
由于p∨q为真命题,p∧q为假命题,则p,q必定为一真一假;
所以$\left\{\begin{array}{l}{-2≤a≤2}\\{a≤-2,或a≥0}\end{array}\right.$,或$\left\{\begin{array}{l}{a<-2,或a>2}\\{-2<a<0}\end{array}\right.$;
∴a=-2或0≤a≤2;
∴实数a的取值范围为{a|0≤a≤2,或a=-2}.
点评 考查函数极值的概念,利用导数判断函数极值的方法,二次函数取值和判别式△的关系,以及函数零点的概念,函数导数符号和函数单调性的关系,以及数形结合解题的方法.

练习册系列答案
相关题目
6.已知向量$\overrightarrow{a}$=(x,-1,-x),向量$\overrightarrow{b}$=(-3,2,x),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数x的值是( )
| A. | -1或2 | B. | 1或-2 | C. | -1或-2 | D. | 1或2 |
3.已知幂函数y=f(x)的图象经过点(2,$\frac{1}{4}$),则它的单调增区间为( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,+∞) |
10.设集合P={x|y=log2x},Q={y|y=x2+1},则P∩Q=( )
| A. | (1,+∞) | B. | [0,+∞) | C. | (0,+∞) | D. | [1,+∞) |