题目内容
9.已知曲线C:f(x)=x3-x+2,求经过点P(1,2)的曲线C的切线方程.分析 设经过点P(1,2)的直线与曲线C相切于点(x0,y0),求导f′(x)=3x2-1,从而可得在点(x0,y0)处的切线的方程为y-y0=(3x02-1)(x-x0).从而得到方程组$\left\{\begin{array}{l}{{y}_{0}={{x}_{0}}^{3}-{x}_{0}+2}\\{2-{y}_{0}=(3{x}_{0}^{2}-1)(1-{x}_{0})}\end{array}\right.$,从而求切线方程.
解答 解:设经过点P(1,2)的直线与曲线C相切于点(x0,y0),
则由f′(x)=3x2-1得:在点(x0,y0)处的斜率k=f′(x0)=3x02-1,
则在点(x0,y0)处的切线的方程为y-y0=(3x02-1)(x-x0).
又因为点(x0,y0)与点P(1,2)均在曲线C上,
所以$\left\{\begin{array}{l}{{y}_{0}={{x}_{0}}^{3}-{x}_{0}+2}\\{2-{y}_{0}=(3{x}_{0}^{2}-1)(1-{x}_{0})}\end{array}\right.$,
消去y0得x0-x03=(3x02-1)(1-x0),
解得x0=1或x0=-$\frac{1}{2}$,
于是k=2或-$\frac{1}{4}$,
所以所求切线方程为y=2x或y=-$\frac{1}{4}$x+$\frac{9}{4}$.
点评 本题考查了导数的几何意义的应用及曲线的切线的求法,属于中档题.

练习册系列答案
相关题目
17.当a=1,b=3时,执行完下面一段程序后x的值是( )
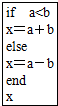
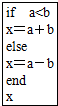
| A. | 1 | B. | 3 | C. | 4 | D. | -2 |