题目内容
6.已知向量$\overrightarrow{a}$=(x,-1,-x),向量$\overrightarrow{b}$=(-3,2,x),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数x的值是( )| A. | -1或2 | B. | 1或-2 | C. | -1或-2 | D. | 1或2 |
分析 根据$\overrightarrow{a}$⊥$\overrightarrow{b}$时$\overrightarrow{a}$•$\overrightarrow{b}$=0,列出方程,求出x的值.
解答 解:∵$\overrightarrow{a}$=(x,-1,-x),$\overrightarrow{b}$=(-3,2,x),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-3x-2-x2=0,
即x2+3x+2=0,
解得x=-1或x=-2,
∴实数x的值是-1或-2.
故选:C.
点评 本题考查了空间向量的坐标运算问题,也考查了用数量积表示垂直的应用问题,是基础题目.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
17.当a=1,b=3时,执行完下面一段程序后x的值是( )
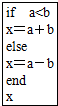
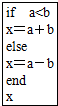
| A. | 1 | B. | 3 | C. | 4 | D. | -2 |
15.等比数列{an}的前项和为Sn,已知S1,2S2,3S3成等差数列,则公比q为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |