题目内容
7.设f(x)是定义在R上的增函数,且对于任意的x都有f(1-x)+f(1+x)=0恒成立,如果?m,n∈R,f(m2-6m+23)+f(n2-8n)<0成立,那么点P(m,n)与圆A:(x-3)2+(y-4)2=4的位置关系是( )| A. | P在圆内 | B. | P在圆上 | C. | P在圆外 | D. | 无法判断 |
分析 由f(1-x)+f(1+x)=0得出f(1-x)=-f(1+x),化简f(m2-6m+23)+f(n2-8n)<0,再由f(x)是R上的增函数,得出m、n的关系式,从而判断点P在圆内.
解答 解:∵对于任意的x都有f(1-x)+f(1+x)=0恒成立,
∴f(1-x)=-f(1+x),
又∵f(m2-6m+23)+f(n2-8n)<0,
∴f(m2-6m+23)<-f[(1+(n2-8n-1)],
∴f(m2-6m+23)<f[(1-(n2-8n-1)]=f(2-n2+8n);
又∵f(x)是R上的增函数,
∴m2-6m+23<2-n2+8n,
∴(m-3)2+(n-4)2<4;
又∵(x-3)2+(y-4)2=4的圆心为(3,4),半径为2,
∴(m-3)2+(n-4)2<4表示圆内的点.
故选:A.
点评 本题考查了函数的性质与应用问题,也考查了点与圆的位置关系的应用问题,是基础题目.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
17.当a=1,b=3时,执行完下面一段程序后x的值是( )
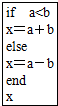
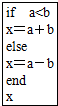
| A. | 1 | B. | 3 | C. | 4 | D. | -2 |
15.等比数列{an}的前项和为Sn,已知S1,2S2,3S3成等差数列,则公比q为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
17.函数f(x)=sin$\frac{2}{3}x+cos\frac{2}{3}$x的图象中相邻的两条对称轴间距离为( )
| A. | $\frac{3}{2}π$ | B. | $\frac{4}{3}π$ | C. | 3π | D. | $\frac{7}{6}π$ |