题目内容
(本小题满分12分)如图:已知正方体ABCD—A1B1C1D1,过BD1的平面分别交棱AA1和棱CC1于E、F两点。(1)求证:A1E=CF; (2)若E、F分别是棱AA1和棱CC1的中点,求证:平面EBFD1⊥平面BB1D1。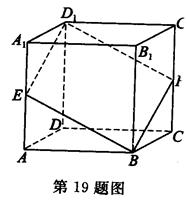

(Ⅰ)见解析 (Ⅱ) 见解析
(1)由题知,平面EBFD1与平面BCC1B1交于
BF、与平面ADD1A交于ED1…………1分
又平面BCC1B1//平面ADD1A1∴D1E//BF …………2分
同理BE//D1F ………………3分∴四边形EBFD1为平行四边形
∴D1E="BF " ……4分∵A1D1==CB,D1E=BF,∠D1A1E=∠BCF=90°
∴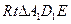 ≌Rt△CBF∴A1E="CF " ………………6分
≌Rt△CBF∴A1E="CF " ………………6分
(2)∵四边形EBFD1是平行四边形。AE=A1E,FC=FC1,
∴Rt△EAB≌Rt△FCB,
∴BE=BF,故四边形EBFD1为菱形。………………8分
连结EF、BD1、A1C1。∵四边形EBFD1为菱形,∴EF⊥BD1,
在正方体ABCD—A1B1C1D1中,有B1D1⊥A1C1,B1D⊥A1A
∴B1D1⊥平面A1ACC1。 ………………10分
又EF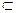 平面A1ACC1,∴EF⊥B1D1。又B1D1∩BD1=D1,
平面A1ACC1,∴EF⊥B1D1。又B1D1∩BD1=D1,
∴EF⊥平面BB1D1。
又EF 平面EBFD1,故平面EBFD1⊥平面BB1D1。 ………………12分
平面EBFD1,故平面EBFD1⊥平面BB1D1。 ………………12分
BF、与平面ADD1A交于ED1…………1分
又平面BCC1B1//平面ADD1A1∴D1E//BF …………2分
同理BE//D1F ………………3分∴四边形EBFD1为平行四边形
∴D1E="BF " ……4分∵A1D1==CB,D1E=BF,∠D1A1E=∠BCF=90°
∴
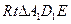 ≌Rt△CBF∴A1E="CF " ………………6分
≌Rt△CBF∴A1E="CF " ………………6分(2)∵四边形EBFD1是平行四边形。AE=A1E,FC=FC1,
∴Rt△EAB≌Rt△FCB,
∴BE=BF,故四边形EBFD1为菱形。………………8分
连结EF、BD1、A1C1。∵四边形EBFD1为菱形,∴EF⊥BD1,
在正方体ABCD—A1B1C1D1中,有B1D1⊥A1C1,B1D⊥A1A
∴B1D1⊥平面A1ACC1。 ………………10分
又EF
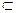 平面A1ACC1,∴EF⊥B1D1。又B1D1∩BD1=D1,
平面A1ACC1,∴EF⊥B1D1。又B1D1∩BD1=D1,∴EF⊥平面BB1D1。
又EF
 平面EBFD1,故平面EBFD1⊥平面BB1D1。 ………………12分
平面EBFD1,故平面EBFD1⊥平面BB1D1。 ………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


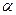 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在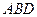 与△
与△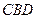 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.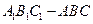 中,
中,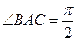 ,
,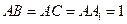 . 已知G与E分别为
. 已知G与E分别为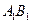 和
和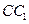 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和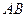 上的动点(不包括端点). 若
上的动点(不包括端点). 若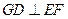 ,则线段
,则线段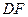 的长度的取值范围为
的长度的取值范围为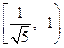



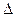 BCD的三条高线的交点;
BCD的三条高线的交点;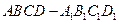 中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA
中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA ="2, " E、E
="2, " E、E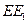 ∥平面
∥平面 ;
; 

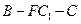 的余弦值
的余弦值
 中,
中,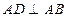 ,
,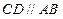 ,
,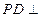 底面
底面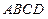 ,
, 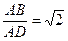 ,直线
,直线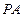 与底面
与底面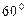 角,点
角,点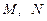 分别是
分别是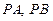 的中点.
的中点.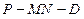 的大小;
的大小;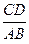 的值为多少时,
的值为多少时,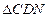 为直角三角形.
为直角三角形.