题目内容
如图三棱柱 中,侧棱
中,侧棱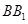 与底面成
与底面成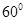 角,
角,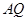 ⊥底面
⊥底面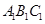 于
于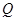 ,
, 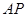 ⊥侧面
⊥侧面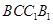 于
于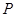 ,且
,且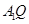 ⊥
⊥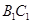 ,
,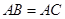 ,
,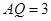 ,
,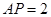 则顶点
则顶点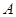 到棱
到棱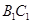 的距离是__________.
的距离是__________.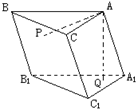
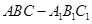 中,侧棱
中,侧棱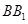 与底面成
与底面成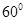 角,
角,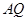 ⊥底面
⊥底面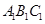 于
于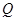 ,
, 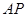 ⊥侧面
⊥侧面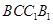 于
于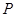 ,且
,且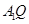 ⊥
⊥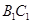 ,
,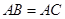 ,
,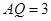 ,
,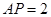 则顶点
则顶点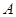 到棱
到棱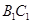 的距离是__________.
的距离是__________.
取B1C1的中点D,连接A1D,PD,先证A、P、D、Q四点共圆,根据余弦定理求出PQ,再根据正弦定理求出直径AD,最后证明AD为顶点A到棱B1C1的距离,即可得到结论.
解:取B1C1的中点D,连接A1D,PD
∵侧棱BB1与底面成60°,A1A∥BB1
∴∠AA1D=60°
而AQ⊥底面A1B1C1于Q,AP⊥侧面BCC1B1于P
∴∠PDQ=120°,∠PAQ=60°
∴A、P、D、Q四点共圆
则AD为圆的直径
根据余弦定理可知PQ= 再根据正弦定理可知2R=
再根据正弦定理可知2R=
∵B1C1⊥面AQD,AD?面AQD
∴B1C1⊥AD
则AD为顶点A到棱B1C1的距离
∴顶点A到棱B1C1的距离为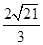
故答案为: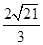
解:取B1C1的中点D,连接A1D,PD
∵侧棱BB1与底面成60°,A1A∥BB1
∴∠AA1D=60°
而AQ⊥底面A1B1C1于Q,AP⊥侧面BCC1B1于P
∴∠PDQ=120°,∠PAQ=60°
∴A、P、D、Q四点共圆
则AD为圆的直径
根据余弦定理可知PQ=
 再根据正弦定理可知2R=
再根据正弦定理可知2R=
∵B1C1⊥面AQD,AD?面AQD
∴B1C1⊥AD
则AD为顶点A到棱B1C1的距离
∴顶点A到棱B1C1的距离为
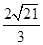
故答案为:
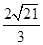

练习册系列答案
相关题目
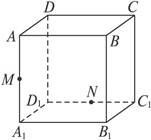
 倍
倍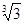 倍
倍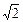 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
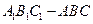 中,
中,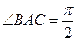 ,
,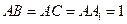 . 已知G与E分别为
. 已知G与E分别为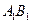 和
和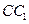 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和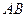 上的动点(不包括端点). 若
上的动点(不包括端点). 若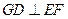 ,则线段
,则线段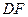 的长度的取值范围为
的长度的取值范围为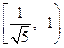



 的各顶点都在球
的各顶点都在球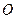 的球面上,其中
的球面上,其中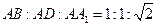 .
.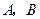 两点的球面距离记为
两点的球面距离记为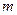 ,
,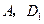 两点的球面距离记为
两点的球面距离记为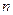 ,则
,则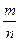 的值为 .
的值为 .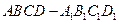 中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA
中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA ="2, " E、E
="2, " E、E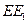 ∥平面
∥平面 ;
; 

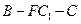 的余弦值
的余弦值
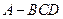 中,棱长为4,
中,棱长为4,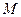 是BC的中点,
是BC的中点,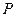 在线段
在线段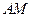 上运动(
上运动(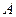 、
、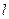
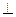 平面
平面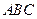 ,
,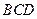 交于点Q,给出下列命题:
交于点Q,给出下列命题: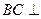 面
面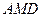
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③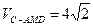
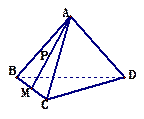
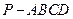 中,底面
中,底面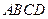 是矩形,
是矩形,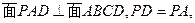
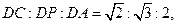
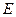 是
是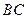 的中点,
的中点,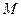 是
是 的中点。
的中点。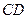 与
与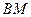 所成的角;(Ⅱ)求二面角
所成的角;(Ⅱ)求二面角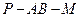 的大小。
的大小。