题目内容
【题目】已知向量 ![]() ,若f(x)=mn. (I)求f(x)的单调递增区间;
,若f(x)=mn. (I)求f(x)的单调递增区间;
(II)己知△ABC的三内角A,B,C对边分别为a,b,c,且a=3,f ![]() ,sinC=2sinB,求A,c,b的值.
,sinC=2sinB,求A,c,b的值.
【答案】解:(I)f(x)=(sinx﹣ ![]() cosx)sin(
cosx)sin( ![]() +x)+
+x)+ ![]() =(sinx﹣
=(sinx﹣ ![]() cosx)cosx+
cosx)cosx+ ![]() =sinxcosx﹣
=sinxcosx﹣ ![]() cos2x+
cos2x+ ![]()
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x=sin(2x﹣
cos2x=sin(2x﹣ ![]() ),
),
令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() 得﹣
得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的单调增区间是[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z.
+kπ],k∈Z.
(II)∵f( ![]() +
+ ![]() )=sin(A﹣
)=sin(A﹣ ![]() )=
)= ![]() ,
,
且﹣ ![]() <A﹣
<A﹣ ![]() <
< ![]() ,
,
∴A﹣ ![]() =
= ![]() ,即A=
,即A= ![]() .
.
∵sinC=2sinB,∴c=2b,
又a=3,由余弦定理得cosA= ![]() =
= ![]() =
= ![]() ,
,
解得b= ![]() ,∴c=2
,∴c=2 ![]() .
.
综上,A= ![]() ,b=
,b= ![]() ,c=2
,c=2 ![]() .
.
【解析】(I)根据平面向量的数量积公式得出f(x)解析式,使用三角恒等变换化简,利用正弦函数的单调性列不等式解出;(II)根据A的范围和f( ![]() )计算A,利用正弦定理和余弦定理求出b,c.
)计算A,利用正弦定理和余弦定理求出b,c.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P 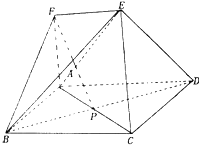
(1)证明:PF∥面ECD;
(2)求二面角B﹣EC﹣A的大小.
【题目】微信是现代生活进行信息交流的重要工具,据统计,某公司![]() 名员工中
名员工中![]() 的人使用微信,其中每天使用微信时间在一小时以内的有
的人使用微信,其中每天使用微信时间在一小时以内的有![]() 人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于
人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于![]() 岁)和中年(年龄不小于
岁)和中年(年龄不小于![]() 岁)两个阶段,使用微信的人中
岁)两个阶段,使用微信的人中![]() 是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中
是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中![]() 是青年人.
是青年人.
(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出![]() 列联表;
列联表;
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(Ⅱ)由列联表中所得数据,是否有![]() 的把握认为“经常使用微信与年龄有关”?
的把握认为“经常使用微信与年龄有关”?
(Ⅲ)采用分层抽样的方法从“经常使用微信”的人中抽取![]() 人,从这
人,从这![]() 人中任选
人中任选![]() 人,求事件
人,求事件![]() “选出的
“选出的![]() 人均是青年人”的概率.
人均是青年人”的概率.
附:
|
|
|
|
|
|


