题目内容
【题目】定义在R上的函数f（x）满足 
， 
．
（1）求函数f（x）的解析式；
（2）求函数g（x）的单调区间；
（3）如果s、t、r满足|s﹣r|≤|t﹣r|，那么称s比t更靠近r．当a≥2且x≥1时，试比较 
和ex﹣1+a哪个更靠近lnx，并说明理由．
【答案】
（1）解：f′（x）=f′（1）e2x﹣2+2x﹣2f（0），所以f′（1）=f′（1）+2﹣2f（0），即f（0）=1．又 
，
所以f′（1）=2e2，所以f（x）=e2x+x2﹣2x．
（2）解：∵f（x）=e2x﹣2x+x2，
∴ 
，
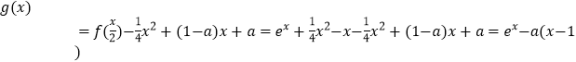∴g′（x）=ex﹣a．
①当a≤0时，g′（x）＞0，函数f（x）在R上单调递增；
②当a＞0时，由g′（x）=ex﹣a=0得x=lna，
∴x∈（﹣∞，lna）时，g′（x）＜0，g（x）单调递减；x∈（lna，+∞）时，g′（x）＞0，g（x）单调递增．
综上，当a≤0时，函数g（x）的单调递增区间为（∞，∞）；
当a＞0时，函数g（x）的单调递增区间为（lna，+∞），单调递减区间为（﹣∞，lna）
（3）解：解：设 
，∵ 
，∴p（x）在x∈[1，+∞）上为减函数，又p（e）=0，∴当1≤x≤e时，p（x）≥0，当x＞e时，p（x）＜0．∵ 
， 
，∴q′（x）在x∈[1，+∞）上为增函数，又q′（1）=0，∴x∈[1，+∞）时，q'（x）≥0，∴q（x）在x∈[1，+∞）上为增函数，∴q（x）≥q（1）=a+1＞0．
① 当1≤x≤e时， 
，
设 
，则 
，∴m（x）在x∈[1，+∞）上为减函数，
∴m（x）≤m（1）=e﹣1﹣a，
∵a≥2，∴m（x）＜0，∴|p（x）|＜|q（x）|，∴ 
比ex﹣1+a更靠近lnx．
②当x＞e时， 
，
设n（x）=2lnx﹣ex﹣1﹣a，则 
， 
，∴n′（x）在x＞e时为减函数，
∴ 
，∴n（x）在x＞e时为减函数，∴n（x）＜n（e）=2﹣a﹣ee﹣1＜0，
∴|p（x）|＜|q（x）|，∴ 比ex﹣1+a更靠近lnx．
综上：在a≥2，x≥1时， 比ex﹣1+a更靠近lnx
【解析】（1）求出函数的导数，利用赋值法，求出f′（1）=f′（1）+2﹣2f（0），得到f（0）=1．然后求解f′（1），即可求出函数的解析式．（2）求出函数的导数g′（x）=ex+a，结合a≥0，a＜0，分求解函数的单调区间即可．（3）构造 ，通过函数的导数，判断函数的单调性，结合当1≤x≤e时，当1≤x≤e时，推出|p（x）|＜|q（x）|，说明 比ex﹣1+a更靠近lnx．当x＞e时，通过作差，构造新函数，利用二次求导，判断函数的单调性，证明 比ex﹣1+a更靠近lnx．
