ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄż(±ŸĐĄÌâÂú·Ö![]() ·Ö)ÒŃÖȘÔČ
·Ö)ÒŃÖȘÔČ![]() ÓĐÒÔÏÂĐÔÖÊŁș
ÓĐÒÔÏÂĐÔÖÊŁș
ąÙčęÔČ![]() ÉÏÒ»”ă
ÉÏÒ»”ă![]() ”ÄÔČ”ÄÇĐÏß·œłÌÊÇ
”ÄÔČ”ÄÇĐÏß·œłÌÊÇ![]() .
.
ąÚÈô![]() ÎȘÔČ
ÎȘÔČ![]() ÍâÒ»”㣏čę
ÍâÒ»”㣏čę![]() ŚśÔČ
ŚśÔČ![]() ”ÄÁœÌőÇĐÏߣŹÇĐ”ă·Ö±đÎȘ
”ÄÁœÌőÇĐÏߣŹÇĐ”ă·Ö±đÎȘ![]() ŁŹÔòÖ±Ïß
ŁŹÔòÖ±Ïß![]() ”Ä·œłÌÎȘ
”Ä·œłÌÎȘ![]() .
.
ąÛÈôČ»ÔÚŚű±êÖáÉϔĔă![]() ÎȘÔČ
ÎȘÔČ![]() ÍâÒ»”㣏čę
ÍâÒ»”㣏čę![]() ŚśÔČ
ŚśÔČ![]() ”ÄÁœÌőÇĐÏߣŹÇĐ”ă·Ö±đÎȘ
”ÄÁœÌőÇĐÏߣŹÇĐ”ă·Ö±đÎȘ![]() ŁŹÔò
ŁŹÔò![]() ŽčÖ±
ŽčÖ±![]() ŁŹŒŽ
ŁŹŒŽ![]() ŁŹÇÒ
ŁŹÇÒ![]() Æœ·ÖÏ߶Î
Æœ·ÖÏ߶Î![]() .
.
(1)Àà±ÈÉÏÊöÓĐčŰœáÂÛŁŹČÂÏëčęÍÖÔČ![]() ÉÏÒ»”ă
ÉÏÒ»”ă![]() ”ÄÇĐÏß·œłÌ(Č»ÒȘÇóրÜ)Ł»
”ÄÇĐÏß·œłÌ(Č»ÒȘÇóրÜ)Ł»
(2)čęÍÖÔČ![]() ÍâÒ»”ă
ÍâÒ»”ă![]() ŚśÁœÖ±ÏߣŹÓëÍÖÔČÏàÇĐÓÚ
ŚśÁœÖ±ÏߣŹÓëÍÖÔČÏàÇĐÓÚ![]() Áœ”㣏Çóčę
Áœ”㣏Çóčę![]() Áœ”ă”ÄÖ±Ïß·œłÌŁ»
Áœ”ă”ÄÖ±Ïß·œłÌŁ»
(3)ÈôčęÍÖÔČ![]() ÍâÒ»”ă
ÍâÒ»”ă![]() Łš
Łš![]() Č»ÔÚŚű±êÖáÉÏŁ©ŚśÁœÖ±ÏߣŹÓëÍÖÔČÏàÇĐÓÚ
Č»ÔÚŚű±êÖáÉÏŁ©ŚśÁœÖ±ÏߣŹÓëÍÖÔČÏàÇĐÓÚ![]() Áœ”㣏ÇóÖ€Łș
Áœ”㣏ÇóÖ€Łș![]() ÎȘ¶šÖ”ŁŹÇÒ
ÎȘ¶šÖ”ŁŹÇÒ![]() Æœ·ÖÏ߶Î
Æœ·ÖÏ߶Î![]() .
.
ĄŸŽđ°žĄżŁš1Ł©![]()
Łš2Ł©![]()
(3)ŒûœâÎö.
ĄŸœâÎöĄż·ÖÎöŁșŁš1Ł©žùŸĘÀà±ÈÍÆÀíżÉ”ĂœáÂÛŁźŁš2Ł©Éè![]() ŁŹœáșÏŁš1Ł©żÉ”Ăčę”ă
ŁŹœáșÏŁš1Ł©żÉ”Ăčę”ă![]() ”ÄÇĐÏß·œłÌŁŹžùŸĘÁœÇĐÏ߶Œčę”ă
”ÄÇĐÏß·œłÌŁŹžùŸĘÁœÇĐÏ߶Œčę”ă![]() żÉ”Ă
żÉ”Ă![]() șÍ
șÍ![]() ŁŹÔÙœáșÏčęÁœ”ă”ÄÖ±ÏßΚһ”ÄÌŰ”ăżÉ”ĂÖ±Ïß
ŁŹÔÙœáșÏčęÁœ”ă”ÄÖ±ÏßΚһ”ÄÌŰ”ăżÉ”ĂÖ±Ïß![]() ”Ä·œłÌÊÇ
”Ä·œłÌÊÇ![]() ŁźŁš3Ł©ÏÈÓÉÖ±Ïß
ŁźŁš3Ł©ÏÈÓÉÖ±Ïß![]() ”Ä·œłÌżÉ”Ă
”Ä·œłÌżÉ”Ă![]() ŁŹÓÖ
ŁŹÓÖ![]() ŁŹËùÒÔ
ŁŹËùÒÔ![]() ŁźÁîÏ߶Î
ŁźÁîÏ߶Î![]() ”ÄÖĐ”ăÎȘ
”ÄÖĐ”ăÎȘ![]() ŁŹÓÉ”ăČî·š”Ă
ŁŹÓÉ”ăČî·š”Ă![]() ŁŹÓÚÊÇ
ŁŹÓÚÊÇ![]() ŁŹčÊ
ŁŹčÊ![]() ŁŹËùÒÔ
ŁŹËùÒÔ![]() Èę”ăčČÏߣŹŽÓ¶ű”Ă”œ
Èę”ăčČÏߣŹŽÓ¶ű”Ă”œ![]() Æœ·ÖÏ߶Î
Æœ·ÖÏ߶Î![]() Łź
Łź
ÏêœâŁșŁš1Ł©čęÍÖÔČ![]() ÉÏÒ»”ă
ÉÏÒ»”ă![]() ”ÄÇĐÏß·œłÌÊÇ
”ÄÇĐÏß·œłÌÊÇ![]() Łź
Łź
Łš2Ł©Éè![]() Łź
Łź
ÓÉŁš1Ł©”ĂčęÍÖÔČÉÏ”ă![]() ”ÄÇĐÏß
”ÄÇĐÏß![]() ”Ä·œłÌÊÇ
”Ä·œłÌÊÇ![]() ŁŹ
ŁŹ
ĄßÖ±Ïß![]() čę”ă
čę”ă![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
ÍŹÀí![]() Łź
Łź
ÓÖčęÁœ”ăA,B”ÄÖ±ÏßÊÇΚһ”ÄŁŹ
ĄàÖ±Ïß![]() ”Ä·œłÌÊÇ
”Ä·œłÌÊÇ![]() Łź
Łź
Łš3Ł©ÓÉŁš2Ł©ÖȘčę![]() Áœ”ă”ÄÖ±Ïß·œłÌÊÇ
Áœ”ă”ÄÖ±Ïß·œłÌÊÇ![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
ÓÖ![]() ŁŹ
ŁŹ
Ąà![]() ÎȘ¶šÖ”Łź
ÎȘ¶šÖ”Łź
Éè![]() Ï߶Î
Ï߶Î![]() ”ÄÖĐ”ăÎȘ
”ÄÖĐ”ăÎȘ![]() ŁŹÔò
ŁŹÔò![]() Łź
Łź
Ąß”ă![]() ŸùÔÚÍÖÔČÉÏŁŹ
ŸùÔÚÍÖÔČÉÏŁŹ
Ąà![]() ąÙŁŹ
ąÙŁŹ![]() ąÚ
ąÚ
ąÚŁąÙ”Ă![]() ŁŹ
ŁŹ
ŒŽ![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
ÓÖ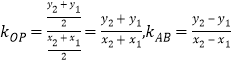
Ąà![]() ŁŹ
ŁŹ
ÓÖ![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąà![]() Èę”ăčČÏߣŹ
Èę”ăčČÏߣŹ
Ąà![]() Æœ·ÖÏ߶Î
Æœ·ÖÏ߶Î![]() Łź
Łź