题目内容
14.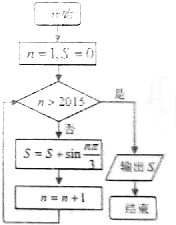 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
分析 根据程序框图的功能,进行求解即可.
解答 解:本程序的计算功能是计算S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sin$\frac{3π}{3}$+…+sin$\frac{2015π}{3}$,
∵y=sin$\frac{nπ}{3}$的周期T=$\frac{2π}{\frac{π}{3}}=6$,且sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sin$\frac{3π}{3}$+…+sin$\frac{6π}{3}$=0,
∴S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sin$\frac{3π}{3}$+…+sin$\frac{2015π}{3}$=sin$\frac{π}{3}$+sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}=\sqrt{3}$,
故选:C
点评 本题主要考查程序框图的识别和判断,了解程序的功能,结合三角函数的周期性是解决本题的关键.

练习册系列答案
相关题目
4.等差数列{an}的前n项和为Sn,如果存在正整数k和l(k≠l),使得Sk=kl2,Sl=lk2,则( )
| A. | Sk+1的最小值为-6 | B. | Sk+l的最大值为-6 | ||
| C. | Sk+1的最小值为6 | D. | Sk+l的最小值为6 |
5.观察下列事实:|x|+|y|≤1的不同整数解(x,y)的个数为5,|x|+|y|≤2 的不同整数解(x,y)的个数为13,|x|+|y|≤3的不同整数解(x,y)的个数为25 ….则|x|+|y|≤20的不同整数解(x,y)的个数为( )
| A. | 841 | B. | 761 | C. | 925 | D. | 941 |
6.下面使用类比推理正确的是( )
| A. | 直线a,b,c,若a∥b,b∥c,则a∥c.类推出:向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,若$\overrightarrow{a}$∥$\overrightarrow{b}$ $\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{c}$. | |
| B. | 同一平面内,直线a,b,c,若a丄c,b丄c,则a∥b.类推出:空间中,直线a,b,c,若a丄c,b丄c,则a∥b. | |
| C. | 若a,b∈R,则a-b>0⇒a>b类推出:若a,b∈C,则a-b>0⇒a>b | |
| D. | 以点(0,0)为圆心,r为半径的圆的方程为x2+y2=r2.类推出:以点(0,0,0)为球心,r为半径的球的方程为x2+y2+z2=r2 |
3.若偶函数f(x)在区间(-∞,0]上单调递减,且f(7)=0,则不等式(x-1)f(x)>0的解集是( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,-7)∪(7,+∞) | C. | (-7,1)∪(7,+∞) | D. | (-7,1]∪(7,+∞) |