题目内容
3.若偶函数f(x)在区间(-∞,0]上单调递减,且f(7)=0,则不等式(x-1)f(x)>0的解集是( )| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,-7)∪(7,+∞) | C. | (-7,1)∪(7,+∞) | D. | (-7,1]∪(7,+∞) |
分析 根据函数奇偶性和单调性之间的关系,将不等式进行转化即可.
解答 解:∵偶函数f(x)在区间(-∞,0]上单调递减,且f(7)=0,
∴f(x)在区间[0,+∞)上单调递增,且f(-7)=f(7)=0,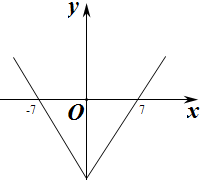
即f(x)对应的图象如图:
则不等式(x-1)f(x)>0等价为:
$\left\{\begin{array}{l}{x>1}\\{f(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<1}\\{f(x)<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x>1}\\{x>7或x<-7}\end{array}\right.$或$\left\{\begin{array}{l}{x<1}\\{-7<x<7}\end{array}\right.$,
即x>7或-7<x<1,
故选:C
点评 本题主要考查不等式的求解,利用函数奇偶性和单调性的性质是解决本题的关键.

练习册系列答案
相关题目
14.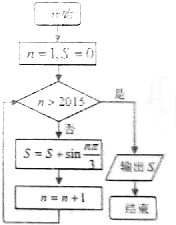 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )
 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
18.函数f(x)=$\sqrt{x-1}$的定义域是( )
| A. | [1,+∞) | B. | (1,+∞) | C. | (0,1) | D. | [0,1] |
8.若函数f(x)=x2-2x+1在区间[a,a+2]上的最小值为4,则a的取值集合为( )
| A. | [-3,3] | B. | [-1,3] | C. | {-3,3} | D. | [-1,-3,3] |
13.若三角形的两内角α,β满足:sinα•cosβ<0,则此三角形的形状为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不能确定 |