题目内容
19.有下列四个命题:①命题“若xy=1,则x,y互为倒数”的逆命题;
②命题“若x≠2或x≠3,则(x-2)(x-3)≠0”的逆否命题;
③命题“若m≤1,则x2-2x+m=0有实根”的逆否命题;
④命题“若A⊆B,则A∩B=B”的逆命题;
其中是真命题的是①③ (填上你认为正确的命题的序号).
分析 ①“若xy=1,则x、y互为倒数”的逆命题为:x、y互为倒数,则xy=1,利用倒数的定义即可判断出;
②“若(x-2)(x-3)=0,则x=2且x=3“不正确;
③若x2-2x+m=0有实根则△=4-4m≥0,解得即可;
④“若A∩B=B,则A⊆B”不正确.
解答 解:对于①,“若xy=1,则x、y互为倒数”的逆命题:“若x、y互为倒数,则xy=1”是真命题,①正确;
对于②,若x≠2或x≠3,则(x-2)(x-3)≠0”的逆否命题;“若(x-2)(x-3)=0,则x=2且x=3”,②不正确;
对于③,若x2-2x+m=0有实根则△=4-4m≥0,解得m≤1,因此正确;它的逆否命题也是真命题,③正确;
对于④,若A⊆B,则A∩B=B”的逆命题:“若A∩B=B,则B⊆A,”④不正确,
综上所述,其中真命题是①③,
故答案为:①③.
点评 本题给出几个命题,要我们找出其中真命题的个数.着重考查了倒数的定义、一元二次方程根的判别式和集合的运算性质等知识,考查了四种命题及其相互关系,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知定义在R上的函数f(x),若f(x)是奇函数,f(x+1)是偶函数,当0≤x≤1时,f(x)=x2,则f(2015)=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 20152 |
14.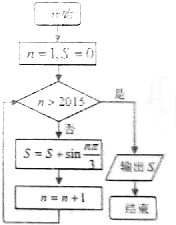 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )
 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
8.若函数f(x)=x2-2x+1在区间[a,a+2]上的最小值为4,则a的取值集合为( )
| A. | [-3,3] | B. | [-1,3] | C. | {-3,3} | D. | [-1,-3,3] |