题目内容
2.定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(-1,4)时,f(x)=x2-2x,则函数f(x)在[0,2015]上的零点个数是605.分析 可判断函数f(x)是定义在R上的周期为10的函数;作出函数f(x)在(-1,9]上的函数图象,从而结合图象判断零点的个数.
解答 解:∵f(x)+f(x+5)=16,
∴f(x+10)+f(x+5)=16;
故f(x)=f(x+10);
故函数f(x)是定义在R上的周期为10的函数;
作函数f(x)在(-1,9]上的函数图象如下,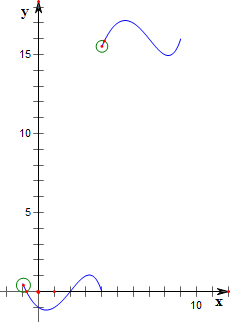
故函数f(x)在(-1,9]上有三个零点;
故函数f(x)在[0,2009]上有3×201-1=602个零点;
在(2009,2015]上有3个零点;
故函数f(x)在[0,2015]上的零点个数是605;
故答案为:605.
点评 本题考查了函数的周期性的判断与应用及函数的图象的作法及数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
12.如图是函数f(x)=x3+bx2+cx+d的大致图象,则x1+x2=( )
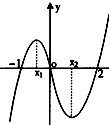

| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
14.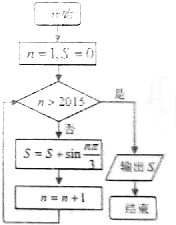 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )
 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |