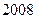题目内容
已知正项数列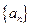 ,其前
,其前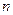 项和
项和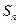 满足
满足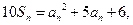 且
且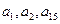 成等比数列,求数列
成等比数列,求数列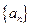 的通项
的通项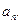
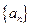 ,其前
,其前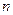 项和
项和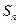 满足
满足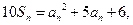 且
且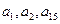 成等比数列,求数列
成等比数列,求数列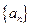 的通项
的通项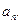
5n-3
解 ∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1="3."
∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1="3."
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)="0 "
∵an+an-1>0 , ∴an-an-1="5" (n≥2).
当a1=3时,a3=13,a15="73." a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3="12," a15="72," 有 a32=a1a15 , ∴a1="2," ∴an=5n-3.
 ∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1="3."
∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1="3." 又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)="0 "
∵an+an-1>0 , ∴an-an-1="5" (n≥2).
当a1=3时,a3=13,a15="73." a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3="12," a15="72," 有 a32=a1a15 , ∴a1="2," ∴an=5n-3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前
的前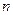 项和.
项和. +
+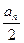 (n∈N+),则其{an}的前10项和为
(n∈N+),则其{an}的前10项和为 ,则
,则
 的前
的前 项和
项和 .
. 中,
中, ,若
,若 项和为
项和为 ,则项数
,则项数