题目内容
已知A,B,C为椭圆W:x2+2y2=2上的三个点,O为坐标原点.
(Ⅰ)若A,C所在的直线方程为y=x+1,求AC的长;
(Ⅱ)设P为线段OB上一点,且|OB|=3|OP|,当AC中点恰为点P时,判断△OAC的面积是否为常数,并说明理由.
(Ⅰ)若A,C所在的直线方程为y=x+1,求AC的长;
(Ⅱ)设P为线段OB上一点,且|OB|=3|OP|,当AC中点恰为点P时,判断△OAC的面积是否为常数,并说明理由.
(Ⅰ)由
,
得3x2+4x=0,
解得x=0或x=-
,
∴A,C两点的坐标为(0,1)和(-
,-
),
∴|AC|=
.
(Ⅱ)①若B是椭圆的右顶点(左顶点一样),则B(
,0),
∵|OB|=3|OP|,P在线段OB上,
∴P(
,0),求得|AC|=
,
∴△OAC的面积等于
×
×
=
.
②若B不是椭圆的左、右顶点,
设AC:y=kx+m(m≠0),A(x1,y1),C(x2,y2),
由
得(2k2+1)x2+4kmx+2m2-2=0,
则x1+x2=-
,x1x2=
,
∴AC的中点P的坐标为(-
,
),
∴B(-
,
),代入椭圆方程,化简得2k2+1=9m2.
计算|AC|=
=
=
.
∵点O到AC的距离dO-AC=
.
∴△OAC的面积S△OAC=
|AC|•dO-AC=
×
•
=
.
综上,△OAC面积为常数
.
|
得3x2+4x=0,
解得x=0或x=-
| 4 |
| 3 |
∴A,C两点的坐标为(0,1)和(-
| 4 |
| 3 |
| 1 |
| 3 |
∴|AC|=
| 4 |
| 3 |
| 2 |
(Ⅱ)①若B是椭圆的右顶点(左顶点一样),则B(
| 2 |
∵|OB|=3|OP|,P在线段OB上,
∴P(
| ||
| 3 |
| 4 |
| 3 |
| 2 |
∴△OAC的面积等于
| 1 |
| 2 |
4
| ||
| 3 |
| ||
| 3 |
| 4 |
| 9 |
②若B不是椭圆的左、右顶点,
设AC:y=kx+m(m≠0),A(x1,y1),C(x2,y2),
由
|
则x1+x2=-
| 4km |
| 2k2+1 |
| 2m2-2 |
| 2k2+1 |
∴AC的中点P的坐标为(-
| 2km |
| 2k2+1 |
| m |
| 2k2+1 |
∴B(-
| 6km |
| 2k2+1 |
| 3m |
| 2k2+1 |
计算|AC|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
2
| ||||||
| 2k2+1 |
8
| ||
| 9|m| |
∵点O到AC的距离dO-AC=
| |m| | ||
|
∴△OAC的面积S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
8
| ||
| 9|m| |
| |m| | ||
|
| 4 |
| 9 |
综上,△OAC面积为常数
| 4 |
| 9 |

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
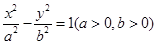 的渐近线与圆
的渐近线与圆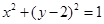 相切,则双曲线离心率为( ).
相切,则双曲线离心率为( ).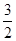
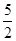
 ,点
,点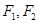 为其两个焦点,点P为双曲线上一点,若
为其两个焦点,点P为双曲线上一点,若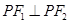 ,则
,则 的值为__________.
的值为__________. 为任何实数,直线
为任何实数,直线 与双曲线
与双曲线 恒有公共点.
恒有公共点. 的离心率
的离心率 的取值范围;
的取值范围; 过双曲线
过双曲线 ,与双曲线交于
,与双曲线交于 两点,并且满足
两点,并且满足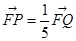 ,求双曲线
,求双曲线