题目内容
【题目】已知过点A(﹣4,0)的动直线l与抛物线C:x2=2py(p>0)相交于B、C两点.
(1)当l的斜率是![]() 时,
时, ![]() ,求抛物线C的方程;
,求抛物线C的方程;
(2)设BC的中垂线在y轴上的截距为b,求b的取值范围.
【答案】
(1)解:设B(x1,y1),C(x2,y2),由已知k1= ![]() 时,l方程为y=
时,l方程为y= ![]() (x+4)即x=2y﹣4.
(x+4)即x=2y﹣4.
由 ![]() 得2y2﹣(8+p)y+8=0
得2y2﹣(8+p)y+8=0
∴ 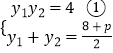 ②
②
又∵ ![]() ,∴y2=4y1③
,∴y2=4y1③
由①②③及p>0得:y1=1,y2=4,p=2,即抛物线方程为:x2=4y
(2)解:设l:y=k(x+4),BC中点坐标为(x0,y0)
由 ![]() 得:x2﹣4kx﹣16k=0④
得:x2﹣4kx﹣16k=0④
∴ ![]() .
.
∴BC的中垂线方程为 ![]()
∴BC的中垂线在y轴上的截距为:b=2k2+4k+2=2(k+1)2
对于方程④由△=16k2+64k>0得:k>0或k<﹣4.
∴b∈(2,+∞)
【解析】(1)先求得直线l的方程,再根据直线与抛物线的位置关系及![]() 求得点B,C的坐标,从而求得抛物线C的方程;(2)设出直线l的方程,利用直线与抛物线的关系表示出BC中点的坐标,则可以表示出BC中垂线的方程,进而表示出BC的中垂线在y轴上的截距,结合直线l的特征求得其截距的取值范围.
求得点B,C的坐标,从而求得抛物线C的方程;(2)设出直线l的方程,利用直线与抛物线的关系表示出BC中点的坐标,则可以表示出BC中垂线的方程,进而表示出BC的中垂线在y轴上的截距,结合直线l的特征求得其截距的取值范围.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目


