Question

【题目】设函数f（x）=x2+2ax﹣a﹣1，x∈[0，2]，a为常数．
（1）用g（x）表示f（x）的最小值，求g（a）的解析式；
（2）在（1）中，是否存在最小的整数m，使得g（a）﹣m≤0对于任意a∈R均成立，若存在，求出m的值；若不存在，请说明理由．

Answer 1

【答案】
（1）解：对称轴 x=﹣a，

①当﹣a＜0即a＞0 时，函数f（x）=x2+2ax﹣a﹣1，x∈[0，2]上是增函数，

当x=0 时有最小值 f（0）=﹣a﹣1

②当﹣a≥2即a≤﹣2 时，函数f（x）=x2+2ax﹣a﹣1，x∈[0，2]上是减函数，

x=2时有最小值，f（2）=3a+3

③当0＜﹣a＜2即﹣2＜a＜0 时，函数f（x）=x2+2ax﹣a﹣1，x∈[0，2]上是不单调，

x=﹣a时有最小值 f（﹣a）=﹣a2﹣a﹣1

∴g（a）=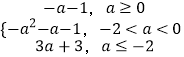

（2）解：存在，由题知g（a）在（﹣∞， ）是增函数，在[ ，+∞）是减函数

a= 时，g（a）max=﹣

g（a）﹣m≤0恒成立，可得g（a）max≤m，∴

∵m为整数，∴m的最小值为0

【解析】（1）先根据二次函数的对称轴对a进行分类讨论，结合函数的单调性进而求得g（a）的解析式；（2）根据（1）中g（a）的解析式判断其单调区间，再求得g（a）的最大值，由g（a）﹣m≤0恒成立，可得g（a）max≤m即可求得整数m的最小值.
【考点精析】认真审题，首先需要了解二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)．