题目内容
已知函数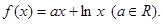
(1)若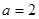 ,求曲线
,求曲线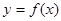 在
在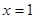 处的切线方程;
处的切线方程;
(2)求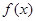 的单调区间;
的单调区间;
(3)设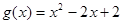 ,若对任意
,若对任意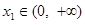 ,均存在
,均存在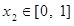 ,使得
,使得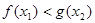 ,求
,求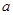 的取值范围.
的取值范围.
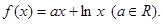
(1)若
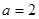 ,求曲线
,求曲线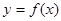 在
在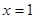 处的切线方程;
处的切线方程;(2)求
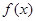 的单调区间;
的单调区间;(3)设
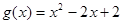 ,若对任意
,若对任意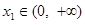 ,均存在
,均存在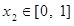 ,使得
,使得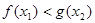 ,求
,求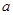 的取值范围.
的取值范围.(1)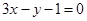 (2)详见解析(3)
(2)详见解析(3)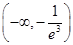
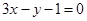 (2)详见解析(3)
(2)详见解析(3)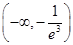
试题分析:
(1)已知函数
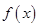 的解析式,把切点的横坐标带入函数
的解析式,把切点的横坐标带入函数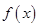 即可求出切点的纵坐标,对
即可求出切点的纵坐标,对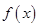 求导得到函数
求导得到函数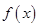 的导函数
的导函数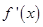 ,把
,把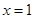 带入导函数
带入导函数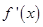 即可求的切线的斜率,利用点斜式即可得到切线的方程.
即可求的切线的斜率,利用点斜式即可得到切线的方程.(2)对函数
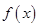 进行求导和求定义域,导函数
进行求导和求定义域,导函数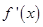 喊参数
喊参数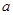 ,把
,把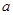 分为两种情况进行讨论,首先
分为两种情况进行讨论,首先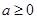 时,结合
时,结合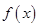 的定义域
的定义域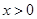 即可得到导函数在定义域内恒大于0,进而得到原函数在定义域内单调递增,当
即可得到导函数在定义域内恒大于0,进而得到原函数在定义域内单调递增,当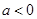 时,求解导函数
时,求解导函数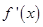 大于0和小于0的解集,得到原函数的单调递增和单调递减区间.
大于0和小于0的解集,得到原函数的单调递增和单调递减区间.(3)该问题为存在性问题与恒成立问题的结合,即要求
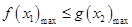 ,而
,而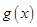 的最大值可以利用二次函数
的最大值可以利用二次函数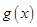 的图像得到函数
的图像得到函数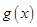 在区间
在区间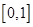 上的最值,函数
上的最值,函数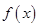 的最大值可以利用第二问的单调性求的,当
的最大值可以利用第二问的单调性求的,当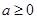 时,函数
时,函数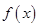 单调递增,无最大值,故不符合题意,当
单调递增,无最大值,故不符合题意,当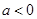 时,函数
时,函数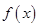 在
在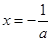 处前的最大值,带入不等式即可求的
处前的最大值,带入不等式即可求的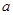 的取值范围.
的取值范围.试题解析:
(1)由已知
 , 1分
, 1分 ,所以斜率
,所以斜率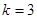 , 2分
, 2分又切点
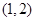 ,所以切线方程为
,所以切线方程为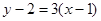 ),即
),即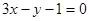
故曲线
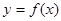 在
在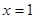 处切线的切线方程为
处切线的切线方程为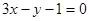 。 3分
。 3分(2)
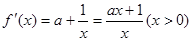 4分
4分①当
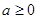 时,由于
时,由于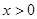 ,故
,故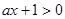 ,
,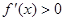 ,所以
,所以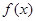 的单调递增区间为
的单调递增区间为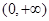 .
.5分
②当
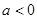 时,由
时,由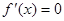 ,得
,得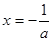 . 6分
. 6分在区间
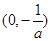 上,
上,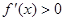 ,在区间
,在区间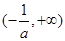 上,
上,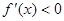 ,
,所以,函数
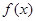 的单调递增区间为
的单调递增区间为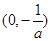 ,单调递减区间为
,单调递减区间为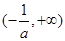 . 7分
. 7分(3)由已知,转化为
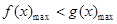 . 8分
. 8分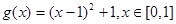 ,所以
,所以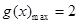 9分
9分由(2)知,当
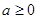 时,
时,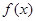 在
在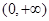 上单调递增,值域为
上单调递增,值域为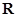 ,故不符合题意.
,故不符合题意.(或者举出反例:存在
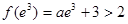 ,故不符合题意.) 10分
,故不符合题意.) 10分当
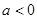 时,
时,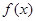 在
在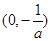 上单调递增,在
上单调递增,在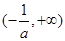 上单调递减,
上单调递减,故
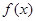 的极大值即为最大值,
的极大值即为最大值,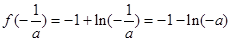 , 12分
, 12分所以
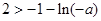 ,解得
,解得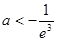 . 14分
. 14分
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
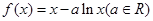
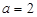 时,求曲线
时,求曲线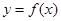 在点
在点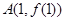 处的切线方程;
处的切线方程;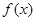 的极值.
的极值.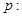 函数
函数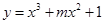 在
在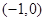 上是单调递减函数,
上是单调递减函数,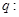 方程
方程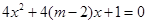 无实根,若“
无实根,若“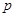 或
或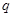 ”为真,“
”为真,“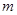 的取值范围。
的取值范围。 与
与 的图象在
的图象在 处有相同的切线,
处有相同的切线, = .
= . ,其中
,其中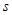 的单位是米,的单位是秒,那么物体在
的单位是米,的单位是秒,那么物体在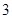 秒末的瞬时速度是( )
秒末的瞬时速度是( )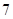 米/秒
米/秒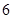 米/秒
米/秒 米/秒
米/秒 米/秒
米/秒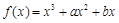 为奇函数,其图象的一条切线方程为
为奇函数,其图象的一条切线方程为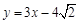 ,则b的值为 .
,则b的值为 .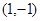 且与曲线
且与曲线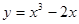 相切的直线方程为( )
相切的直线方程为( )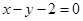 或
或