题目内容
已知椭圆
 的离心率为
的离心率为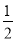 ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆C的标准方程;
(2)若直线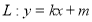 与椭圆
与椭圆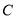 相交于
相交于 、
、 两点,且
两点,且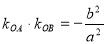 ,求证:
,求证: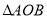 的面积为定值并求出定值
的面积为定值并求出定值
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
题目内容
已知椭圆
 的离心率为
的离心率为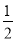 ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆C的标准方程;
(2)若直线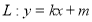 与椭圆
与椭圆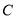 相交于
相交于 、
、 两点,且
两点,且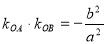 ,求证:
,求证: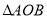 的面积为定值并求出定值
的面积为定值并求出定值
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案