题目内容
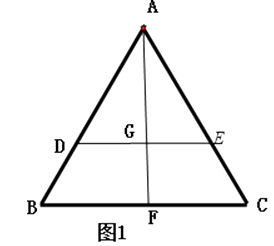
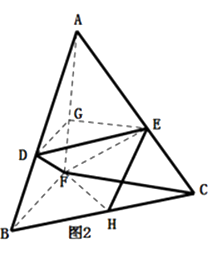
【题目】如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC上的点,AD=AE,F是BC的中点,AF与DE交于点G,△ABF沿AF折起,得到如图2所示的三棱锥A﹣BCF,其中BC= ![]() .
. 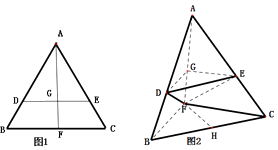
(1)求证:平面DEG∥平面BCF;
(2)若D,E为AB,AC上的中点,H为BC中点,求异面直线AB与FH所成角的余弦值.
【答案】
(1)证明:如题图1,在等边三角形ABC中,AB=AC,
∵AD=AE,∴ ![]() ,
,
∴DE∥BC,∴DG∥BF,
如题图2,∵DG平面BCF,
∴DG∥平面BCF,
同理可证EG∥平面BCF,
∵DG∩EG=G,
∴平面DEG∥平面BCF
(2)解:连EH,
∵EH是△CAB的中位线,
∴ ![]()
∴异面直线AB与FH所成角即为∠FHE
∵ ![]()
∴△BFC为RT△,∴ ![]() ,
,
又∵ ![]()
∴cos∠FHE= ![]() =
= 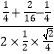 =
= ![]()
【解析】 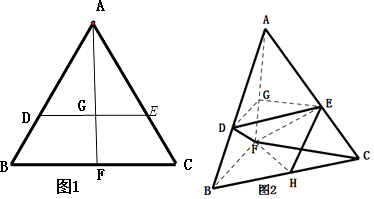
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系,以及对平面与平面平行的判定的理解,了解判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行.

 高效智能课时作业系列答案
高效智能课时作业系列答案【题目】某批次的某种灯泡![]() 个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命 (天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)根据频率分布表中的数据,写出![]() 的值;
的值;
(2)某人从这![]() 个灯泡中随机地购买了
个灯泡中随机地购买了![]() 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率;
(3)某人从这批灯泡中随机地购买了![]() 个,如果这
个,如果这![]() 个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求![]() 的最小值.
的最小值.
【题目】如图,棱长为2的正方体ABCD﹣A1B1C1D1中,E为边AA1的中点,P为侧面BCC1B1上的动点,且A1P∥平面CED1 . 则点P在侧面BCC1B1轨迹的长度为( ) 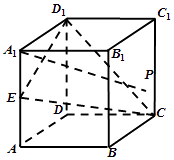
A.2
B.![]()
C.![]()
D.![]()