题目内容
【题目】如图，棱长为2的正方体ABCD﹣A1B1C1D1中，E为边AA1的中点，P为侧面BCC1B1上的动点，且A1P∥平面CED1 ． 则点P在侧面BCC1B1轨迹的长度为（ ）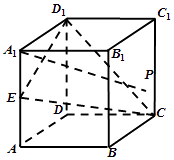 
A.2
B.
C.
D.
【答案】C
【解析】解：取C1D1 ， C1C的中点G，F， 
连接A1G、FG，BF，A1B，
∵GF∥D1C，GF平面CED1 ， GF∥平面CED1 ，
BF∥D1E，BF平面CED1 ， BF∥平面CED1 ，
∵BF，GF是平面A1GFB内的相交直线，
∴平面A1GFB∥平面CED1 ，
故A1P∥平面CED1时，
P在侧面BCC1B1的轨迹是线段BF，
∵正方体ABCD﹣A1B1C1D1的棱长为2，
故BF= 
，
故选：C
【考点精析】关于本题考查的空间中直线与平面之间的位置关系，需要了解直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点才能得出正确答案．
练习册系列答案
相关题目
【题目】观察研究某种植物的生长速度与温度的关系，经过统计，得到生长速度（单位：毫米/月）与月平均气温的对比表如下：
温度 | -5 | 0 | 6 | 8 | 12 | 15 | 20 |
生长速度 | 2 | 4 | 5 | 6 | 7 | 8 | 10 |
（1）求生长速度
关于温度
的线性回归方程；（斜率和截距均保留为三位有效数字）；
（2）利用（1）中的线性回归方程，分析气温从
至
时生长速度的变化情况，如果某月的平均气温是
时，预测这月大约能生长多少．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
．
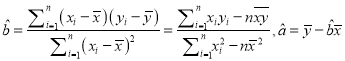