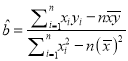题目内容
【题目】函数![]() 在它的某一个周期内的单调减区间是
在它的某一个周期内的单调减区间是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)将![]() 的图象先向右平移
的图象先向右平移![]() 个单位,再将图象上所有点的横坐标变为原来的
个单位,再将图象上所有点的横坐标变为原来的![]() 倍(纵坐标不变),所得到的图象对应的函数记为
倍(纵坐标不变),所得到的图象对应的函数记为![]() ,若对于任意的
,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求三角函数的解析式,可根据![]() 的性质求解,条件“一个周期内的单调减区间是
的性质求解,条件“一个周期内的单调减区间是![]() ”,可得周期,最大值和最小值,由此可求得
”,可得周期,最大值和最小值,由此可求得![]() ;(2)由三角函数图象变换可得
;(2)由三角函数图象变换可得![]() 的解析式,从而能求得
的解析式,从而能求得![]() 在
在![]() 上的最大值和最小值,
上的最大值和最小值,![]() ,等价于
,等价于![]() ,即
,即![]() ,因此只要有
,因此只要有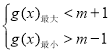 ,由此可得
,由此可得![]() 的范围.
的范围.
试题解析:(1)由条件,![]() ,∴
,∴![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() ,∴
,∴![]() 的解析式为
的解析式为![]() .
.
(2)将![]() 的图象先向右平移
的图象先向右平移![]() 个单位,得
个单位,得![]() ,∴
,∴![]() ,
,
而![]() ,∴
,∴![]() ,∴函数
,∴函数![]() 在
在![]() 上的最大值为1,此时
上的最大值为1,此时![]() ,∴
,∴![]() ;最小值为
;最小值为![]() ,此时
,此时![]() ,∴
,∴![]() .
.
![]() 时,不等式
时,不等式![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
即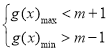 ,∴
,∴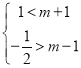 ,∴
,∴![]() .
.

练习册系列答案
相关题目