题目内容
【题目】已知命题p:存在实数m,使方程x2+mx+1=0有两个不等的负根;命题q:存在实数m,使方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
【答案】m≥3或1<m≤2.
【解析】
试题分析:利用一元二次方程的实数根与判别式的关系、不等式的解法可得命题P与Q的m的取值范围,再由“P或Q”为真,“P且Q”为假,可得P与Q必然一个为真一个为假.即可得出
试题解析:存在实数m,使方程x2+mx+1=0有两个不等的负根,则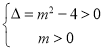 ,解得m>2,即m>2时,p真.
,解得m>2,即m>2时,p真.
存在实数m,使方程4x2+4(m-2)x+1=0无实根,
则Δ=16(m-2)2-16=16(m2-4m+3)<0,
解得1<m<3,即1<m<3时,q真.
因“p或q”为真,所以命题p、q至少有一个为真,
又“p且q”为假,所以命题p、q至少有一个为假,
因此,命题p、q应为一真一假,即命题p为真,命题q为假或命题p为假,命题q为真.
∴![]() 或
或![]() ,解得m≥3或1<m≤2.
,解得m≥3或1<m≤2.
所以m的取值范围是m≥3或1<m≤2

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 |
| 0.1 |
第2组 |
| 0.1 |
第3组 |
| 0.4 |
第4组 |
| 0.3 |
第5组 |
| 0.1 |
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
