Question

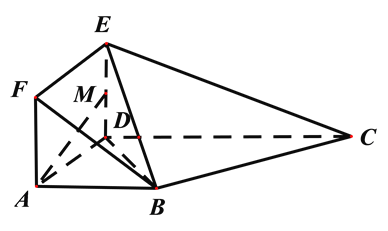
【题目】如图，在多面体中，平面与平面垂直，是正方形，在直角梯形中，，，且，为线段的中点.

（1）求证：平面；

（2）求证：平面；

（3）求三棱锥的体积.

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）.

【解析】试题分析: (1)取中点,利用三角形中位线及已知条件,可证四边形为平行四边形,再利用线线平行得到线面平行;(2)由梯形中各边的数量关系,利用勾股定理,可得,又由已知条件可得,则由线面垂直的判定定理可得结论;(3)三棱锥也就是三棱锥,易求,可得.

试题解析：（1）取中点,连接,

三角形中,,

则四边形为平行四边形,

则,

又,,则;

(2)在梯形中,,可得三角形为直角三角形,

其中;

又平面与平面垂直,是正方形,则 ,

所以,

又,

则 ;

（3）.