题目内容
9.△ABC的外接圆圆心为O,半径为2,$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow 0$,且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|,$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为( )| A. | -3 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 由题意,得到四边形OCAB是边长为2的菱形,$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为对角线BC的一半.
解答 解:由题意,$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow 0$,得到$\overrightarrow{OB}+\overrightarrow{AC}=\overrightarrow{0}$,又|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|=|$\overrightarrow{OB}$|,△OAB是等边三角形,所以四边形OCAB是边长为2的菱形,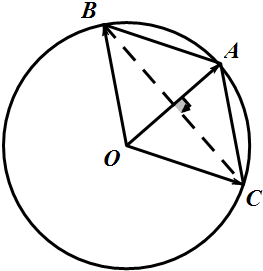
所以$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为ACcos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$;
故选C.
点评 本题考查了向量的投影;解得本题的关键是由题意,画出图形,明确四边形OBAC的形状,利用向量解答.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
18.现有六本书,其中两本相同,其余四本各不相同,分成三堆,每堆两本,则不同的分法的种数为( )
| A. | 9种 | B. | 12种 | C. | 15种 | D. | 18种 |
19.不等式|x-1|-|x-5|<2的解集是( )
| A. | (-∞,4) | B. | (-∞,1) | C. | (1,4) | D. | (1,5) |

 如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是
如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是 如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.
如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.